(5) Double Machine Learning

Causal Data Science for Business Analytics

Christoph Ihl

Hamburg University of Technology

Monday, 24. June 2024

Preliminaries

Observed Confounding

• We need these assumptions:

Assumption A1: “Conditional Exchangeability / Unconfoundedness / Ignorability / Independence”.

\(Y_i(t) \perp\!\!\!\perp T_i \mid \mathbf{X_i = x}, \forall t \in \{0,1,\dots\}, \text{ and } \mathbf{x} \in \mathbb{X}\).

Assumption A2: “Positivity / Overlap / Common Support”.

\(0 < P(T_i = t|\mathbf{X_i = x}), \forall t \in \{0,1,\dots\}, \text{ and } \mathbf{x} \in \mathbb{X}\).

Assumption A3: “Stable Unit Treatment Value Assumption (SUTVA).”

\(Y_i = Y(T_i)\)

• … to achieve identification of the ATE:

Theorem: “Identification of the ATE”:

\(\tau_{\text{ATE}} = \mathbb{E}[Y_i(1)] - \mathbb{E}[Y_i(0)] = \mathbb{E_X}[\mathbb{E}[Y_i|T_i=1,\mathbf{X_i = x}] - \mathbb{E}[Y_i|T_i=0, \mathbf{X_i = x}]]\)

Types of Parameters

Causal Machine Learning methods force us to distinguish between two types of parameters:

• 1. Target parameter is motivated by the research question and defined under modelling assumption,
  • e.g. effect of a treatment on some outcome.
• 2. Nuisance parameters are inputs that are required to obtain the target parameter, but are not relevant for our research question.
  • e.g. propensity scores.
• Focus on the target parameter and do not get tempted to interpret every single coefficient from a regression.

Frisch-Waugh-Lovell (FWL) Theorem

• We can estimate \(\beta_T\) in a standard linear regression \(Y_i = \beta_0 + \beta_T T_i + \mathbf{\beta_{X}' X_i} + \epsilon_i\) in a three-stage procedure:

1. Run a regression of the form \(Y_i = \beta_{Y0} + \mathbf{\beta_{Y \sim X}' X_i} + \epsilon_{Y_i \sim X_i}\) and extract the estimated residuals \(\hat\epsilon_{Y_i \sim X_i}\).

2. Run a regression of the form \(T_i = \beta_{T0} + \mathbf{\beta_{T \sim X}' X_i} + \epsilon_{T_i \sim X_i}\) and extract the estimated residuals \(\hat\epsilon_{T_i \sim X_i}\).

3. Run a residual-on-residual regression of the form \(\hat\epsilon_{Y_i \sim X_i} = \beta_T \hat\epsilon_{T_i \sim X_i} + \epsilon_i\) (no constant).

The resulting estimate \(\hat\beta_T\) is numerically identical to the estimate we would get if we just run the full OLS model.

Target Parameters

• Average potential outcome (APO): \(\mu_t := \mathbb{E}[Y_i(t)]\).
  • What is the expected outcome if everybody receives treatment t?
• Average Treatment Effect (ATE): \(\tau_{\text{ATE}} := \mathbb{E}[Y_i(1)] - \mathbb{E}[Y_i(0)] = \mu_1 - \mu_0\).
  • What is the expected treatment effect in the population?

• Note that the target parameters are just different aggregations of the Conditional Average Potential Outcome (CAPO): \(\mathbb{E}[Y_i(t) \mid \mathbf{X_i = x} ]\)
  • \(\mu_t := \mathbb{E}[Y_i(t)] \overset{LIE}{=} \mathbb{E}[\mathbb{E}[Y_i(t) \mid \mathbf{X_i = x}]]\)
  • \(\tau_{\text{ATE}} := \mathbb{E}[Y_i(1)] - \mathbb{E}[Y_i(0)] \overset{LIE}{=} \mathbb{E}[\mathbb{E}[Y_i(1) \mid \mathbf{X_i = x}]] - \mathbb{E}[\mathbb{E}[Y_i(0) \mid \mathbf{X_i = x} ]]\).
• It suffices to show that the CAPO is identified.

General Approach

• Causal Machine Learning methods are mostly about rewriting stuff such that we are allowed to leverage supervised ML to estimate the nuisance parameters.
• Importantly, the target parameters of interest remain the same although the rewritten form can look quite different to the original/familiar model.
• The methods usually boil down to running multiple supervised ML regressions and combining their predictions into a final OLS regression.
• Supervised ML holds the promise of data-driven model selection and complex non-linear relationships, and thus, getting (one of) the nuisance parameters right.
• The crucial point is that the statistical inference in this final OLS regression is valid if we follow a particular recipe.
  • Recipe of how to split the estimation of causal effects into prediction tasks.

Doubly Robust Methods

Doubly Robust Methods: Idea

• Given the three assumptions hold, we have seen two ways to identify the ATE: \(\tau_{\text{ATE}} = \mathbb{E}[Y_i(1)] - \mathbb{E}[Y_i(0)] = \mu_1 - \mu_0\)

• Conditional outcome regression:
  • \(\tau_{\text{ATE}} = \mathbb{E_X}[\mathbb{E}[Y_i | T_i = 1, \mathbf{X_i = x}] - \mathbb{E}[Y_i | T_i = 0, \mathbf{X_i = x}]]\)
  • Simplified notation with nuisance parameter \(\mu(t, \mathbf{x}) = \mathbb{E}[Y_i | T_i = t, \mathbf{X_i = x}]\) as conditional average potential outcome:
  • \(\tau_{\text{ATE}} = \mathbb{E_X}[\mu(t = 1, \mathbf{x}) - \mu(t=0,\mathbf{x})]\)

• Inverse probability weighting:
  • \(\tau_{\text{ATE}} = \mathbb{E}\left[\frac{T_i Y_i}{P(T_i = 1 \mid \mathbf{X_i = x})}\right] - \mathbb{E}\left[\frac{(1 - T_i) Y_i}{1 - P(T_i = 1 \mid \mathbf{X_i})}\right]\)
  • \(\tau_{\text{ATE}} = \mathbb{E}\left[\frac{T_i Y_i}{PS(\mathbf{X_i})}\right] - \mathbb{E}\left[\frac{(1 - T_i) Y_i}{1 - PS(\mathbf{X_i})}\right]\)
  • Simplified notation with nuisance parameter \(e_t(\mathbf{x}) = P(T_i = t \mid \mathbf{X_i = x})\) as propensity score:
  • \(\tau_{\text{ATE}} = \mathbb{E}\left[\frac{\mathbb{1}(T_i = 1) Y_i}{e_{t=1}(\mathbf{x})}\right] - \mathbb{E}\left[\frac{\mathbb{1}(T_i = 0) Y_i}{e_{t=0}(\mathbf{x})}\right]\)

• Idea of doubly robust methods:
  • Combine both approaches, such that the ATE estimator is consistent, even if only one of the two models is correctly specified.

Doubly Robust Estimator: Definition

• Doubly robust or Augmented Inverse Propensity Score Weighting (AIPW) estimator:
• Conditional average potential outcome (CAPO) given by:

\[ \begin{align*} \mu_t^{\text{AIPW}}(\mathbf{x}) := \mathbb{E}[Y_i(t) | \mathbf{X_i = x}] &\overset{(A1,A3)}{=} \mathbb{E}[Y_i | T_i = 0, \mathbf{X_i = x}] := \mu(t, \mathbf{x}) \\ &\text{(conditional outcome regression)} \\ &\overset{(2)}{=} \mathbb{E}\left[\frac{\mathbb{1}(T_i = t)Y_i}{e_t(x)} \bigg| \mathbf{X_i = x}\right] \\ &\text{(inverse probability weighting)} \\ &\overset{(3)}{=} \mathbb{E}\bigg[\mu(t, \mathbf{x}) + \frac{\mathbb{1}(T_i = t)(Y_i - \mu(t, \mathbf{x}))}{e_t(\mathbf{x})} \bigg| \mathbf{X_i = x}\bigg] \\ &\text{(augmenting outcome regression with IPW weights)} \\ \end{align*} \]

• Average potential outcome (APO) given by:

  \[\mu_t^{\text{AIPW}} = \mathbb{E_x}\bigg[\mathbb{E}\bigg[\mu(t, \mathbf{x}) + \frac{\mathbb{1}(T_i = t)(Y_i - \mu(t, \mathbf{x}))}{e_t(\mathbf{x})} \bigg| \mathbf{X_i = x}\bigg] \bigg] = \mathbb{E}\bigg[\mu(t, \mathbf{x}) + \frac{\mathbb{1}(T_i = t)(Y_i - \mu(t, \mathbf{x}))}{e_t(\mathbf{x})} \bigg] \\\]

Doubly Robust Estimator: Proof

• Proof for Equation (2):

\[ \begin{align*} \mu_t(\mathbf{x}) := \mathbb{E}[Y_i(t) | \mathbf{X_i = x}] &= \mathbb{E}[Y_i | T_i = 0, \mathbf{X_i = x}]\\ &= \mathbb{E}[\underbrace{\mathbb{1}(T_i = t)}_{=1} Y_i \mid T_i = t, \mathbf{X_i = x}]\\ &= \mathbb{E}\left[ \mathbb{1}(T_i = t) \frac{e_t(\mathbf{x})}{e_t(\mathbf{x})} \mid {T_i = t, \mathbf{X_i = x}}\right] + (1 - e_t(\mathbf{x})) \mathbb{E}[\underbrace{\mathbb{1}(T_i = t)}_{=0} Y_i \mid T_i \neq t, \mathbf{X_i = x}]/e_t(\mathbf{x})\\ &= \frac{\overbrace{e_t(\mathbf{x}) \mathbb{E}[\mathbb{1}(T_i = t) Y_i \mid T_i = t, \mathbf{X_i = x}] + (1 - e_t(\mathbf{x})) \mathbb{E}[\mathbb{1}(T_i = t) Y_i \mid T_i \neq t, \mathbf{X_i = x}]}^{\overset{LIE}{=}\mathbb{E}[\mathbb{1}(T_i = t) Y_i | \mathbf{X_i = x}]}}{e_t(\mathbf{x})} \\ &= \frac{\mathbb{E}\left[\mathbb{1}(T_i = t)Y_i \mid \mathbf{X_i = x} \right]}{e_t(\mathbf{x})} = \mathbb{E}\left[\frac{\mathbb{1}(T_i = t)Y_i}{e_t(\mathbf{x})} \bigg| \mathbf{X_i = x}\right] \end{align*} \]

Doubly Robust Estimator: Proof

• Proof for Equation (3):

\[ \begin{align*} \mu_t(\mathbf{x}) := \mathbb{E}[Y_i(t) | \mathbf{X_i = x}] &= \mathbb{E}\left[\mu(t, \mathbf{x}) + \frac{\mathbb{1}(T_i = t)(Y_i - \mu(t, \mathbf{x}))}{e_t(\mathbf{x})} \bigg| \mathbf{X_i = x}\right] \\ &= \mathbb{E}\left[Y_i(t) - Y_i(t) + \mu(t, \mathbf{x}) + \frac{\mathbb{1}(T_i = t)(Y_i - \mu(t, \mathbf{x}))}{e_t(\mathbf{x})} \bigg| \mathbf{X_i = x}\right] \\ &= \mathbb{E}\left[Y_i(t) - Y_i(t) + \mu(t, \mathbf{x}) + \frac{\mathbb{1}(T_i = t)(Y_i(t) - \mu(t, \mathbf{x}))}{e_t(\mathbf{x})} \bigg| \mathbf{X_i = x}\right] \\ &= \mathbb{E}[Y_i(t) \mid \mathbf{X_i = x}] + \mathbb{E} \left[(Y_i(t) - \mu(t, \mathbf{x})) \bigg(\frac{\mathbb{1}(T_i = t) - e_t(\mathbf{x})}{e_t(\mathbf{x})}\bigg) \bigg| \mathbf{X_i = x} \right] \\ &\overset{(4)}{=} \mu_t(\mathbf{x}) + \underbrace{\mathbb{E} \left[ (Y_i(t) - \mu(t, \mathbf{x})) \bigg(\frac{\mathbb{1}(T_i = t) - e_t(\mathbf{x})}{e_t(\mathbf{x})}\bigg) \bigg| \mathbf{X_i = x} \right]}_{\text{needs to be 0 for the conditional APO to be identified}} \end{align*} \]

Doubly Robust Estimator: Proof

• Proof for Equation (4):

• Let \(\tilde{\mu}(t,\mathbf{x})\) and \(\tilde{e}_{t}(\mathbf{x})\) be some candidate functions for the conditional outcome regression and the propensity score, respectively.

\[ \begin{align*} \mathbb{E} \left[ (Y_i(t) - \tilde{\mu}(t, \mathbf{x})) \bigg(\frac{\mathbb{1}(T_i = t) - \tilde{e}_t(\mathbf{x})}{\tilde{e}_t(\mathbf{x})}\bigg) \bigg| \mathbf{X_i = x} \right] &= \mathbb{E} [ (Y_i(t) - \tilde{\mu}(t, \mathbf{x})) \mid \mathbf{X_i = x}] \mathbb{E} \left[ \bigg(\frac{\mathbb{1}(T_i = t) - \tilde{e}_t(\mathbf{x})}{\tilde{e}_t(\mathbf{x})}\bigg) \bigg| \mathbf{X_i = x} \right] \\ &\text{(ignorability allows to separate expectations)} \\ &= (\mathbb{E} [ Y_i(t) \mid \mathbf{X_i = x}] - \tilde{\mu}(t, \mathbf{x})) \bigg(\frac{\mathbb{E} [\mathbb{1}(T_i = t \mid \mathbf{X_i = x} ] - \tilde{e}_t(\mathbf{x})}{\tilde{e}_t(\mathbf{x})}\bigg) \\ &= (\mu_t(\mathbf{x}) - \tilde{\mu}(t, \mathbf{x})) \frac{(e_t(\mathbf{x}) - \tilde{e}_t(\mathbf{x}))}{\tilde{e}_t(\mathbf{x})} \\ \end{align*} \]

• the last expression becomes 0 if either \(\tilde{\mu}(t, \mathbf{x}) = \mu_t(\mathbf{x})\) or \(\tilde{e}_t(\mathbf{x}) = e_t(\mathbf{x})\).

Doubly Robust Estimator: Theorem

• Augmentation leads to the following theoretical properties:

Theorem 4.3: “Doubly Robust Estimator”.

Given \(Y_i(t) \perp\!\!\!\perp T_i \mid \mathbf{X_i = x}\) (conditional unconfoundedness) and given \(0 < P(T_i = t|\mathbf{X_i = x}), \forall t\) (positivity), then:

1. If either \(\tilde{e}_{t}(\mathbf{x}) = e_t(\mathbf{x})\) or \(\tilde{\mu}(t = 1,\mathbf{x}) = \mu_1(\mathbf{x})\), then \(\mu_{1} = \mathbb{E}[Y_i(1)]\)

2. If either \(\tilde{e}_{t}(\mathbf{x}) = e_t(\mathbf{x})\) or \(\tilde{\mu}(t = 0,\mathbf{x}) = \mu_0(\mathbf{x})\), then \(\mu_{0} = \mathbb{E}[Y_i(0)]\)

3. If either \(\tilde{e}_{t}(\mathbf{x}) = e_t(\mathbf{x})\) or \(\tilde{\mu}(t = 1,\mathbf{x}) = \mu_1(\mathbf{x}), \tilde{\mu}(t = 0,\mathbf{x}) = \mu_0(\mathbf{x})\), then \(\mu_{1} - \mu_{0} = \tau_{\text{ATE}}\)

• with \(\tilde{\mu}(t,\mathbf{x})\) and \(\tilde{e}_{t}(\mathbf{x})\) being some candidate functions for the conditional outcome regression and the propensity score, respectively.

Doubly Robust Estimator: Theorem

• Proof showing that \(\mu_{t} = \mathbb{E}[Y_i(t)]\):

\[ \begin{align*} \tilde{\mu}_{t} - \mathbb{E}[Y_i(t)] &= \mathbb{E}\bigg[\tilde{\mu}(t, \mathbf{x}) + \frac{\mathbb{1}(T_i = t)(Y_i - \tilde{\mu}(t, \mathbf{x}))}{\tilde{e}_t(\mathbf{x})} \bigg] - \mathbb{E}[Y_i(t)] &\text{(by defintion)} \\ &= \mathbb{E}\bigg[\frac{\mathbb{1}(T_i = t)(Y_i - \tilde{\mu}(t, \mathbf{x}))}{\tilde{e}_t(\mathbf{x})} - (Y_i(t) - \tilde{\mu}(t, \mathbf{x}))\bigg] &\text{(linearity of expectations)} \\ &= \mathbb{E}\left[\frac{\mathbb{1}(T_i = t) - \tilde{e}_t(\mathbf{x})}{\tilde{e}_t(\mathbf{x})}(Y_i(t) - \tilde{\mu}(t, \mathbf{x}))\right] &\text{(combining terms)} \\ &= \mathbb{E}\left(\mathbb{E}\left[\frac{\mathbb{1}(T_i = t) - \tilde{e}_t(\mathbf{x})}{\tilde{e}_t(\mathbf{x})}(Y_i(t) - \tilde{\mu}(t, \mathbf{x}) \bigg| \mathbf{X_i}\right]\right) &\text{(law of iterated expectations)} \\ &= \mathbb{E}\left(\mathbb{E}\left[\frac{\mathbb{1}(T_i = t) - \tilde{e}_t(\mathbf{x})}{\tilde{e}_t(\mathbf{x})} \bigg| \mathbf{X_i}\right] \cdot \mathbb{E}\left[Y_i(t) - \tilde{\mu}(t, \mathbf{x}) \bigg| \mathbf{X_i}\right]\right) &\text{(ignorability allows to separate expectations)} \\ &= \mathbb{E}\left( \frac{(e_t(\mathbf{x}) - \tilde{e}_t(\mathbf{x}))}{\tilde{e}_t(\mathbf{x})}(\mu_t(\mathbf{x}) - \tilde{\mu}(t, \mathbf{x}))\right) \\ \end{align*} \]

Doubly Robust Estimator: Sample Version

• Step 1: obtain the fitted values of the propensity scores:
  • \(\hat{e}_t(\mathbf{X_i})\)
• Step 2: obtain the fitted values of the outcome regressions:
  • \(\hat{\mu}(t, \mathbf{X_i})\).
• Step 3: construct the doubly robust estimator:

  • \(\hat{\tau}_{\text{ATE}} = \hat{\mu}_{1} - \hat{\mu}_{0}\) with

  • \(\hat{\mu}_{1} = \frac{1}{n} \sum_{i=1}^n \left[\hat{\mu}(t= 1, \mathbf{X_i}) + \frac{\mathbb{1}(T_i = 1)(Y_i - \hat{\mu}(t = 1, \mathbf{ X_i})}{\hat{e}_1(\mathbf{X_i})}\right]\)

  • \(\hat{\mu}_{0} = \frac{1}{n} \sum_{i=1}^n \left[\hat{\mu}(t= 0, \mathbf{X_i}) + \frac{\mathbb{1}(T_i = 0)(Y_i - \hat{\mu}(t = 0, \mathbf{ X_i})}{\hat{e}_0(\mathbf{X_i})}\right]\)

Doubly Robust Estimator: Example

• Assess the impact of participating in the U.S. National Supported Work (NSW) training program targeted to 445 individuals with social and economic problems on their real earnings.

library(Matching)                       # load Matching package
data(lalonde)                           # load lalonde data
attach(lalonde)                         # store all variables in own objects
library(drgee)                          # load drgee package
T = treat                              # define treatment (training)
Y = re78                                # define outcome 
X = cbind(age,educ,nodegr,married,black,hisp,re74,re75,u74,u75) # covariates
dr = drgee(oformula = formula(Y ~ X), eformula = formula(T ~ X), elink="logit") # DR reg
summary(dr)                             # show results

Call:  drgee(oformula = formula(Y ~ X), eformula = formula(T ~ X), elink = "logit")

Outcome:  Y 

Exposure:  T 

Covariates:  Xage,Xeduc,Xnodegr,Xmarried,Xblack,Xhisp,Xre74,Xre75,Xu74,Xu75 

Main model:  Y ~ T 

Outcome nuisance model:  Y ~ Xage + Xeduc + Xnodegr + Xmarried + Xblack + Xhisp + Xre74 + Xre75 + Xu74 + Xu75 

Outcome link function:  identity 

Exposure nuisance model:  T ~ Xage + Xeduc + Xnodegr + Xmarried + Xblack + Xhisp + Xre74 + Xre75 + Xu74 + Xu75 

Exposure link function:  logit 

  Estimate Std. Error z value Pr(>|z|)  
T   1674.1      672.4    2.49   0.0128 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Note: The estimated parameters quantify the conditional
exposure-outcome association, given the covariates
included in the nuisance models)

 445  complete observations used

Double Machine Learning with Partially Linear Regression

Partially Linear Regression Model

• Observed \(Y_i\) and \(T_i\) are a partially linear function of confounding variables \(X_i\): \(\begin{align}\begin{aligned}Y_i = \tau T_i + g(\mathbf{X_i}) + \epsilon_{Y_i}, & &\mathbb{E}(\epsilon_{Y_i} | T_i,\mathbf{X_i}) = 0 \\T_i = e(\mathbf{X_i}) + \epsilon_{T_i}, & &\mathbb{E}(\epsilon_{T_i} | \mathbf{X_i}) = 0\end{aligned}\end{align}\)

• Conditional average potential outcome:
  • \(\mathbb{E}[Y_i(t) | \mathbf{X_i}] \overset{(A1, A3)}{=} \mathbb{E}[Y_i | T_i = t, \mathbf{X_i}] = \tau t + g(\mathbf{X_i})\)

• Target parameters:
  • \(\tau_{\text{CATE}} = \mathbb{E}[Y_i | T_i = 1, \mathbf{X_i}] - \mathbb{E}[Y_i | T_i = 0, \mathbf{X_i}]\)
  • \(\tau_{\text{CATE}} = (\tau 1 + g(\mathbf{X_i})) - (\tau 0 + g(\mathbf{X_i})) = \tau\)
  • \(\tau_{\text{ATE}} = \mathbb{E_X}[\beta_T] = \tau\)
  • => homogeneous treatment effects

Identification under Partial Linearity

• Following Robinson (1988), we can write the partially linear regression model as a generalization of the Frisch-Waugh-Lovell theorem:
  • \(\underbrace{Y_i - \overbrace{\mathbb{E}[Y_i \mid \mathbf{X_i}]}^{\mu(\mathbf{X_i})}}_{\text{outcome residual}} = \tau \underbrace{( T_i - \overbrace{\mathbb{E}[T_i \mid \mathbf{X_i}]}^{e(\mathbf{X_i})})}_{\text{treatment residual}} + \epsilon_{Y_i}\)

• \(\tau_{\text{ATE}}\) is identified by a residual-on-residual regression without constant:
  • Population estimand:
    • \(\tau_{\text{ATE}} = \arg \min_{\tilde{\tau}} \mathbb{E}[( \underbrace{ Y_i - \mu(\mathbf{X_i})}_{\text{pseudo outcome}} - \tilde{\tau} \underbrace{( T_i - e(\mathbf{X_i}))}_{\text{single regressor}})^2] = \frac{\text{Cov}[(Y_i - \mu(\mathbf{X_i})) (T_i - e(\mathbf{X_i}))]}{\text{Var}[T_i - e(\mathbf{X_i})]}\)
  • Sample estimator:
    • \(\hat{\tau}_{\text{ATE}} = \arg \min_{\tilde{\tau}} \frac{1}{N}\sum_{i=1}^n ( \underbrace{Y_i - \hat{\mu}(\mathbf{X_i})}_{\text{pseudo outcome}} - \tilde{\tau} \underbrace{( T_i - \hat{e}(\mathbf{X_i}))}_{\text{single regressor}})^2 = \frac{\sum_{i=1}^n (Y_i - \hat{\mu}(\mathbf{X_i})) (T_i - \hat{e}(\mathbf{X_i}))}{\sum_{i=1}^n (T_i - \hat{e}(\mathbf{X_i}))^2}\)

• However, regression not feasible because nuisance parameters unknown: ML toolbox might be useful.

Double Machine Learning under Partial Linearity

• Chernozhukov et al. (2018) propose a three step procedure:

  1. Form prediction model for the treatment: \(\hat{e}(\mathbf{X_i})\)

  2. Form prediction model for the outcome: \(\hat{\mu}(\mathbf{X_i})\)

  3. Run feasible residual-on-residual regression:

  • \(\hat{\tau}_{\text{ATE}} = \arg \min_{\tilde{\tau}} \frac{1}{N}\sum_{i=1}^n ( Y_i - \hat{\mu}(\mathbf{X_i}) - \tilde{\tau} ( T_i - \hat{e}(\mathbf{X_i})))^2 = \frac{\sum_{i=1}^n (Y_i - \hat{\mu}(\mathbf{X_i})) (T_i - \hat{e}(\mathbf{X_i}))}{\sum_{i=1}^n (T_i - \hat{e}(\mathbf{X_i}))^2}\)

• Predictions of nuisance parameters \(\hat{e}(\mathbf{X_i})\) and \(\hat{\mu}(\mathbf{X_i})\) have to fulfill two conditions:
  1. High-quality: consistency and convergence rates faster than \(N^{\frac{1}{4}}\).
  2. Out-of-sample: individual predictions formed without the observation itself.
  => standard (robust) OLS inference is valid (see Chernozhukov et al. (2018)).

High Quality Predictions in DML

• Consistency: ML methods converge to the true nuisance parameters as \(N \to \infty\).
• Convergence rate:
  • Parametric models like OLS converge at the rate \(N^{\frac{1}{2}}\):
    • RMSE (\(\mathbb{E}[\sqrt{(\hat{\mu}(\mathbf{X_i}) - \mu(\mathbf{X_i}))^2}]\)) expected to halve if sample increases by factor four
  • ML methods usually do not converge as quickly because they can not leverage the structural information of a parametric model.
  • For Double ML to work, it suffices that the RMSE more than halves if we increase sample size by factor 16 (convergence rate: \(N^{\frac{1}{4}}\)).
  • Achievable with popular ML methods like (Post-) LASSO, Random Forests, or Neural Networks .

Out-of-Sample Predictions in DML

• K-fold Cross-Fitting:
  • Split the sample into \(K\) folds.
  • For each fold \(k\), train a prediction model for the nuisance parameters on the remaining \(K-1\) folds.
  • Predict the nuisance parameters for fold \(k\) using the model trained on the remaining \(K-1\) folds.
  • Repeat for all \(K\) folds to obtain predictions for each individual observation in each fold.
  • Use combined predictions for the residual-on-residual regression.

=> Predictions are formed without the observation itself, still no waste of information.

=> Nuisance parameters induce no bias by overfitting (Chernozhukov et al. (2018)).

Neyman-orthogonal Score Functions

• Predicted nuisance parameters have to be used in a Neyman-orthogonal score function (score) \(\psi\)!
• \(\psi\) has to satisfy moment condition \(\mathbb{E}[\psi(Y_i,T_i,\hat{\tau}, \hat{\mu}(\mathbf{X_i}), \hat{e}(\mathbf{X_i}))] = 0\) to identify the target parameter \(\tau_{\text{ATE}}\).
• In PLR, \(\psi\) is the solution to the minimization problem of the residual-on-residual regression - derivative w.r.t. \(\hat{\tau}\):

\[\begin{align*} &\frac{1}{N} \sum_{i=1}^N \underbrace{(Y_i - \hat{\mu}(\mathbf{X_i}) - \hat{\tau}(T_i - \hat{e}(\mathbf{X_i}))) (T_i - \hat{e}(X_i))}_{\psi(Y_i, T_i, \hat{\tau}, \hat{\mu}(\mathbf{X_i}), \hat{e}(\mathbf{X_i}))} = 0 \\ \Rightarrow \hat{\tau}_{\text{ATE}} &= \frac{\sum_{i=1}^n (Y_i - \hat{\mu}(\mathbf{X_i})) (T_i - \hat{e}(\mathbf{X_i}))}{\sum_{i=1}^n (T_i - \hat{e}(\mathbf{X_i}))^2} \end{align*}\]

• Neyman-orthogonality of score \(\psi(Y_i,T_i,\hat{\tau}, \hat{\mu}(\mathbf{X_i}), \hat{e}(\mathbf{X_i}))\):
  • (Gateaux) derivative of the score function with respect to the nuisance parameters is zero in expectation at the true value of the nuisance parameters:
    • \(\partial_r \mathbb{E}[\psi(Y_i, T_i, \hat{\tau}, \mu(\mathbf{X_i}) + r(\mu(\mathbf{X_i}) - \hat{\mu}(\mathbf{X_i})), e(\mathbf{X_i}) + r(e(\mathbf{X_i}) - \hat{e}(\mathbf{X_i})))]\mid_{r=0} = 0\)
  • Ensures that the \(\hat{\tau}\) is robust against biases in the prediction of nuisance parameters (e.g. by regularization).
  • Note (without proof): residual-on-residual regression fulfills this requirement!

Overcoming Regularization & Overfitting Bias

• Compare a non-orthogonal score function, e.g. \(\hat{\tau}_{\text{ATE}} = \frac{\sum_{i=1}^n T_i (Y_i - \hat{\mu}(\mathbf{X_i}))}{\sum_{i=1}^n T_i^2}\) to orthogonal one: \(\hat{\tau}_{\text{ATE}} = \frac{\sum_{i=1}^n (Y_i - \hat{\mu}(\mathbf{X_i})) (T_i - \hat{e}(\mathbf{X_i}))}{\sum_{i=1}^n (T_i - \hat{e}(\mathbf{X_i}))^2}\).

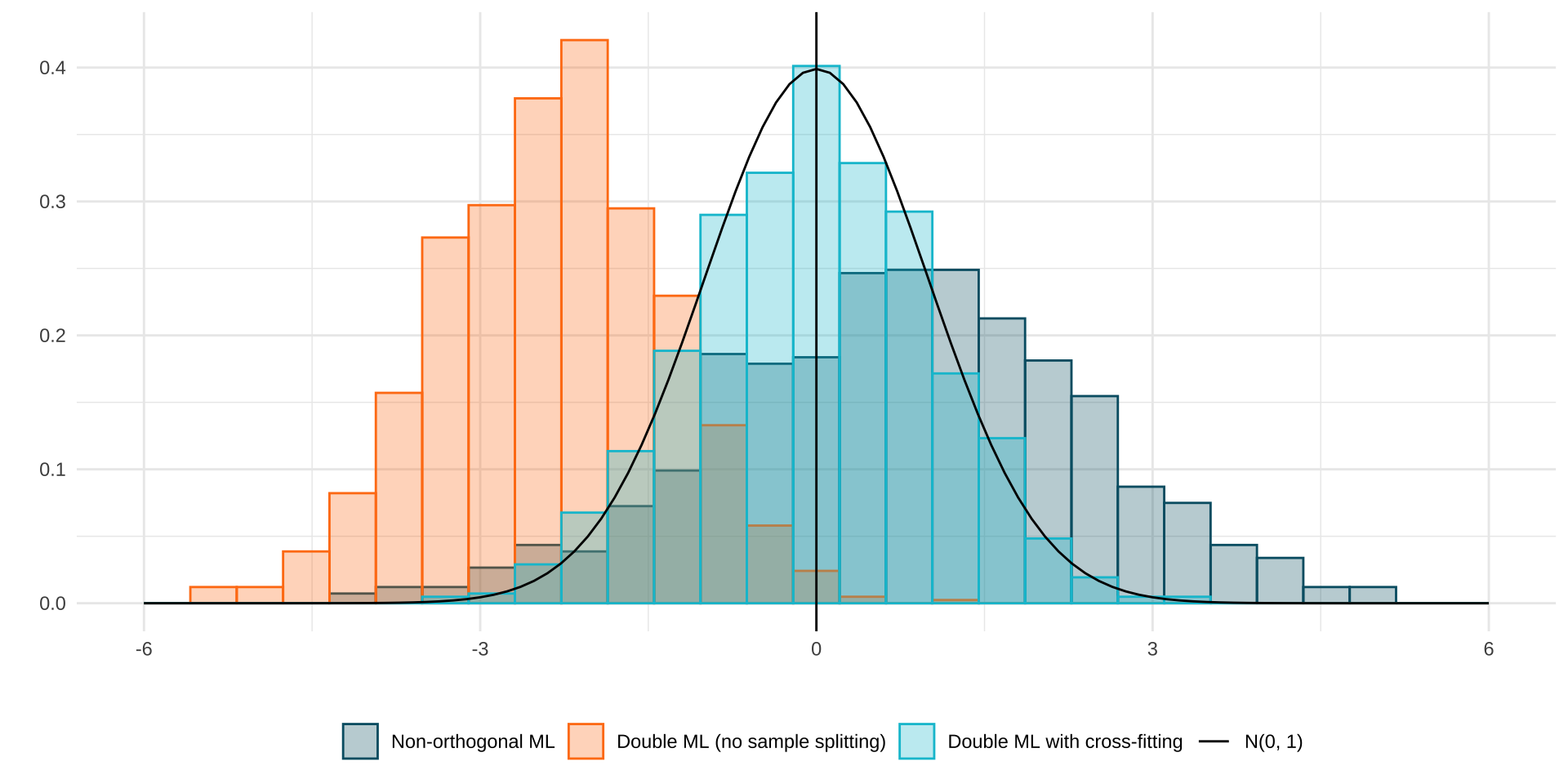
• Compare with and without K-fold Cross-Fitting.

# simulating the data
library(DoubleML)
set.seed(1234)
n_rep = 1000 # number samples
n_obs = 500 # number of observations
n_vars = 20 # number of covariates
alpha = 0.5 # true treatment effect


data = list()
for (i_rep in seq_len(n_rep)) {
# command to simulate Y_i and T_i based on true non-linear nuisance functions m(x) and e(x)
  data[[i_rep]] = make_plr_CCDDHNR2018(alpha=alpha, n_obs=n_obs, dim_x=n_vars,
                                       return_type="data.frame")
}

# define custom (non-othogonal) score function
non_orth_score = function(y, d, l_hat, m_hat, g_hat, smpls) {
  u_hat = y - g_hat
  psi_a = -1*d*d
  psi_b = d*u_hat
  psis = list(psi_a = psi_a, psi_b = psi_b)
  return(psis)
}

library(mlr3)
library(mlr3learners)

# define the ml prediction models from the mlr3 package:
ml_l = lrn("regr.ranger", num.trees = 132, max.depth = 5, mtry = 12, min.node.size = 1) # learner for mu = E[Y|X]
ml_m = lrn("regr.ranger", num.trees = 378, max.depth = 3, mtry = 20, min.node.size = 6) # learner for e = E[T|X]


# run the simulation 
for (i_rep in seq_len(n_rep)) {
  df = data[[i_rep]]
  obj_dml_data = double_ml_data_from_data_frame(df, y_col = "y", d_cols = "d")
  # key function friom the DoubleML package
  obj_dml_plr_nonorth = DoubleMLPLR$new(obj_dml_data, # suppy data
                                        ml_l, ml_m, ml_g,# supply the machine learning methods
                                        n_folds=2, # no cross fitting at first
                                        score=non_orth_score, # supply custom score function
                                        # score='partialling out' # built-in orthogonal score function PLM
                                        apply_cross_fitting=TRUE) # no cross fitting at first
  # extract and store estimates for each sample
  obj_dml_plr_nonorth$fit()
  this_theta = obj_dml_plr_nonorth$coef
  this_se = obj_dml_plr_nonorth$se
  print(abs(theta_nonorth[i_rep] - this_theta))
  print(abs(se_nonorth[i_rep] - this_se))
  theta_nonorth[i_rep] = this_theta
  se_nonorth[i_rep] = this_se
}

Double Machine Learning with Augmented Inverse Probability Weighting

Interactive Regression Model

• More general model that relaxes the homogeneous treatment assumption (binary \(T_i\) is not additively separable anymore): \(\begin{align}\begin{aligned}Y_i = \mu(T_i, \mathbf{X_i}) + \epsilon_{Y_i}, & &\mathbb{E}(\epsilon_{Y_i} | T_i,\mathbf{X_i}) = 0 \\T_i = e(\mathbf{X_i}) + \epsilon_{T_i}, & &\mathbb{E}(\epsilon_{T_i} | \mathbf{X_i}) = 0\end{aligned}\end{align}\)

• We can use the identification results from the Doubly Robust / AIPW estimator:
  • Average potential outcome (APO):
    • \(\mu_t^{\text{AIPW}} = \mathbb{E}[Y_i(t)] = \mathbb{E}\bigg[\mu(t, \mathbf{X_i}) + \frac{\mathbb{1}(T_i = t)(Y_i - \mu(t, \mathbf{X_i}))}{e_t(\mathbf{X_i})} \bigg] \\\)
  • Average treatment effect (ATE):
    • \(\tau_{\text{ATE}}^{\text{AIPW}} = \mathbb{E}[Y_i(1) - Y_i(0)] = \mathbb{E}\bigg[\mu(1, \mathbf{X_i}) - \mu(0, \mathbf{X_i}) + \frac{T_i(Y_i - \mu(1, \mathbf{X_i}))}{e_1(\mathbf{X_i})} - \frac{(1-T_i)(Y_i - \mu(0, \mathbf{X_i})}{e_0(\mathbf{X_i}))} \bigg]\)

Double Machine Learning under AIPW

• Chernozhukov et al. (2018) propose a three step procedure:

  1. Form prediction model for the treatment: \(\hat{e}(\mathbf{X_i})\)

  2. Form prediction model for the outcome: \(\hat{\mu}(T_i, \mathbf{X_i})\)

  3. 1. Estimate the APO:
  • \(\hat{\mu}_t^{\text{AIPW}} = \frac{1}{N}\sum_{i=1}^n \bigg(\hat{\mu}(t, \mathbf{X_i}) + \frac{\mathbb{1}(T_i = t)(Y_i - \hat{\mu}(t, \mathbf{X_i}))}{\hat{e}_t(\mathbf{X_i})} \bigg) \\\)
  3. 2. Estimate the ATE:
  • \(\hat{\tau}_{\text{ATE}}^{\text{AIPW}} = \frac{1}{N}\sum_{i=1}^n \bigg(\hat{\mu}(1, \mathbf{X_i}) - \hat{\mu}(0, \mathbf{X_i}) + \frac{T_i(Y_i - \hat{\mu}(1, \mathbf{X_i}))}{\hat{e}_1(\mathbf{X_i})} - \frac{(1-T_i)(Y_i - \hat{\mu}(0, \mathbf{X_i})}{\hat{e}_0(\mathbf{X_i}))} \bigg)\)

• To obtain a consistent, asymptotically normal and semi-parametrically efficient estimator that allows standard (robust) inference, we need the same three key ingredients:
  1. High-quality machine learning methods
  2. K-fold cross-validation
  3. Neyman-orthogonal score function: let’s proof this!

DML-AIPW Score Function (1)

• As the score defining the ATE is just the difference between APOs, it inherits ist Neyman orthogonality. Hence let’s focus on the AIPW score of the APO, which is:

\[\begin{align*} &\mathbb{E}\bigg[ \underbrace{\mu(t, \mathbf{X_i}) + \frac{\mathbb{1}(T_i = t)(Y_i - \mu(t, \mathbf{X_i}))}{e_t(\mathbf{X_i})} - \mu_t^{\text{AIPW}}}_{\psi(Y_i, T_i, \mu(t, \mathbf{X_i}), e(\mathbf{X_i}))}\bigg] = 0 \\ \Rightarrow \mu_t^{\text{AIPW}} = & \mathbb{E}\bigg[\mu(t, \mathbf{X_i}) + \frac{\mathbb{1}(T_i = t)(Y_i - \mu(t, \mathbf{X_i}))}{e_t(\mathbf{X_i})} \bigg] \end{align*}\]

• Neyman-orthogonality of a score \(\psi\) means that the Gateaux derivative with respect to the nuisance parameters is zero in expectation at the true nuisance parameters (NP). This means:

\[\partial_r \mathbb{E}\left[\psi(Y_i, T_i, \mu + r(\tilde{\mu}-\mu), e + r(\tilde{e} - e)) \mid \mathbf{X_i = x}\right] |_{r=0} = 0\]

• where we suppress the dependencies of NPs and denote by, e.g., \(\tilde{\mu}\) a value of the outcome nuisance that is different to the true value \(\mu\). We can show this equation holds with the following four steps.

DML-AIPW Score Function (2)

• 1. Add perturbations to the true nuisance parameters in the score:

\[ \begin{align*} \psi&(Y_i, T_i, \mu + r(\tilde{\mu} - \mu), e + r(\tilde{e} - e)) \\ &= (\mu + r(\tilde{\mu} - \mu)) + \frac{ \mathbb{1}(T_i = t) Y_i}{e + r(\tilde{e} - e)} - \frac{\mathbb{1}(T_i = t) (\mu + r(\tilde{\mu} - \mu))}{e + r(\tilde{e} - e)} - \mu_t^{\text{AIPW}} \end{align*} \]

• 2. Take the conditional expectation:

\[ \begin{align*} &\mathbb{E}\left[ \psi(Y_i, T_i, \mu + r(\tilde{\mu} - \mu), e + r(\tilde{e} - e)) \mid \mathbf{X_i = x} \right] \\ &= \mathbb{E}\left[ (\mu + r(\tilde{\mu} - \mu)) + \frac{ \mathbb{1}(T_i = t) Y_i}{e + r(\tilde{e} - e)} - \frac{\mathbb{1}(T_i = t) (\mu + r(\tilde{\mu} - \mu))}{e + r(\tilde{e} - e)} - \mu_t^{\text{AIPW}} \bigg| \mathbf{X_i = x} \right] \\ &= (\mu + r(\tilde{\mu} - \mu)) + \frac{ e\mu}{e + r(\tilde{e} - e)} - \frac{e (\mu + r(\tilde{\mu} - \mu))}{e + r(\tilde{e} - e)} - \mu_t^{\text{AIPW}} \end{align*} \] - where we use that \(\mathbb{E}[\mathbb{1}(T_i = t)Y_i \mid \mathbf{X_i = x}] \overset{(A3)}{=} \mathbb{E}[\mathbb{1}(T_i = t)Y_i(t) \mid \mathbf{X_i = x}] \overset{(A1)}{=} e\mu\) and \(\mathbb{E}[\mathbb{1}(T_i = t) \mid \mathbf{X_i = x}] = e\).

DML-AIPW Score Function (3)

• 3. Take the derivative with respect to \(r\):

\[ \begin{align*} \frac{\partial}{\partial r} &\mathbb{E}[\psi(Y_i, T_i, \mu + r(\tilde{\mu} - \mu), e + r(\tilde{e} - e)) \mid X_i = x] \\ &= (\tilde{\mu} - \mu) - \frac{e\mu(\tilde{e} - e)}{(e + r(\tilde{e} - e))^2} - \frac{e(\tilde{\mu} - \mu)(e+r(\tilde{e} - e)) - e(\mu + r(\tilde{\mu} - \mu))(\tilde{e} - e)}{(e + r(\tilde{e} - e))^2} \end{align*} \]

• 4. Evaluate at the true nuisance values, i.e. set \(r = 0\):

\[ \begin{align*} \frac{\partial}{\partial r} &\mathbb{E}[\psi(Y_i, T_i, \mu + r(\tilde{\mu} - \mu), e + r(\tilde{e} - e)) \mid X_i = x] |_{r=0} \\ &= (\tilde{\mu} - \mu) - \frac{e\mu(\tilde{e} - e)}{(e + 0(\tilde{e} - e))^2} - \frac{e(\tilde{\mu} - \mu)(e+r(\tilde{e} - e)) - e(\mu + 0(\tilde{\mu} - \mu))(\tilde{e} - e)}{(e + 0(\tilde{e} - e))^2} \\ &= (\tilde{\mu} - \mu) - \frac{e\mu(\tilde{e} - e)}{e^2} - \frac{e(\tilde{\mu} - \mu)e - e\mu(\tilde{e} - e)}{e^2} \\ &= (\tilde{\mu} - \mu) - \frac{e\mu(\tilde{e} - e)}{e^2} - \frac{e^2}{e^2}(\tilde{\mu} - \mu) + \frac{e\mu(\tilde{e} - e)}{e^2}\\ &= 0 \end{align*} \]

DML-AIPW: Example

• Assess the effect of 401(k) program participation on net financial assets of 9,915 households in the US in 1991.

# Load required packages
library(DoubleML)
library(mlr3)
library(mlr3learners)
library(data.table)

# suppress messages during fitting
lgr::get_logger("mlr3")$set_threshold("warn")

# load data as a data.table
data = fetch_401k(return_type = "data.table", instrument = TRUE)

# Set up basic model: Specify variables for data-backend
features_base = c("age", "inc", "educ", "fsize","marr", "twoearn", "db", "pira", "hown")

# Initialize DoubleMLData (data-backend of DoubleML)
data_dml_base = DoubleMLData$new(data,
                                 y_col = "net_tfa", # outcome variable
                                 d_cols = "e401", # treatment variable
                                 x_cols = features_base) # covariates

# Initialize Random Forrest Learner
randomForest = lrn("regr.ranger")
randomForest_class = lrn("classif.ranger")

# Random Forest
set.seed(123)
dml_irm_forest = DoubleMLIRM$new(data_dml_base,
                                 ml_g = randomForest,
                                 ml_m = randomForest_class,
                                 score = "ATE",
                                 trimming_threshold = 0.01,
                                 apply_cross_fitting = TRUE,
                                 n_folds = 5)

# Set nuisance-part specific parameters
dml_irm_forest$set_ml_nuisance_params(
    "ml_g0", "e401", list(max.depth = 6, mtry = 4, min.node.size = 7)) # learner for outcome 0
dml_irm_forest$set_ml_nuisance_params(
    "ml_g1", "e401", list(max.depth = 6, mtry = 3, min.node.size = 5)) # learner for outcome 1
dml_irm_forest$set_ml_nuisance_params( 
    "ml_m", "e401", list(max.depth = 6, mtry = 3, min.node.size = 6)) # learner for treatment

dml_irm_forest$fit()
dml_irm_forest$summary()

Estimates and significance testing of the effect of target variables
     Estimate. Std. Error t value Pr(>|t|)    
e401      8206       1106   7.421 1.16e-13 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

General Recipe

Definitions

• Data and parameters;
  • \(W\) is a set of observed variables; e.g., \(W = \{Y, T, X\}\).
  • \(\theta\) is the target parameter.
  • \(\eta\) is a set of nuisance parameters; e.g., \(\eta = \{\mu(X), e(X)\}\).

• Score functions \(\psi(W, \tilde{\theta}, \tilde{\eta})\) must satisfy two properties in Double ML:
  • \(\mathbb{E}[\psi(W, \theta, \eta)] = 0\): i.e. moment condition with expectation zero if evaluated at true parameters.
  • \(\partial_r\mathbb{E}[\psi(W, \theta, \eta + r(\hat{\eta} - \eta))]|_{r=0} = 0\): i.e. Neyman-orthogonality.

Examples

• Moment condition of the residual-on-residual regression:
  • \(\mathbb{E} \left[ (Y - \mu(X) - \tau (T - e(X))) (T - e(X)) \right] = 0\)
  • \(W = (T, X, Y), \quad \theta = \tau, \quad \eta = (\mu(X), e(X))\)
  • with \(\mu(X) := \mathbb{E}[Y \mid X]\) and \(e(X) := \mathbb{E}[T \mid X]\)

• Moment condition of the AIPW-ATE:
  • \(\mathbb{E} \left[ \mu(1, X) - \mu(0, X) + \frac{T(Y - \mu(1,X))}{e(X)} - \frac{(1 - T)(Y - \mu(0, X))}{1 - e(X)} - \tau_{ATE} \right] = 0\)
  • \(W = (T, X, Y), \quad \theta = \tau_{\text{ATE}}, \quad \eta = (\mu(1, X), \mu(0, X), e(X))\)
  • with \(\mu(t,X) := \mathbb{E}[Y \mid T = t, X]\) and \(e(X) := \mathbb{E}[T=1 \mid X]\)

Linear Score Functions

• We will focus on linear score functions that can be represented as follows:
  • \(\psi(W, \tilde{\theta}, \tilde{\eta}) = \tilde{\theta}\psi_a(W, \tilde{\eta}) + \psi_b(W, \tilde{\eta})\)
• such that the moment condition can be written as:
  • \(\mathbb{E}[\psi(W, \theta, \eta)] = \theta \mathbb{E}[\psi_a(W, \eta)] + \mathbb{E}[\psi_b(W, \eta)] = 0\)
• and the solution is:
  • \(\theta = - \frac{\mathbb{E}[\psi_b(W, \eta)]}{\mathbb{E}[\psi_a(W, \eta)]}\)

Example Residual-on-residual Regression

• Moment condition:

\[ \begin{align*} \mathbb{E} \left[ (Y - \mu(X) - \tau(T - e(X)))(T - e(X)) \right] &= 0 \\ \mathbb{E} \left[ (Y - \mu(X))(T - e(X)) - \tau(T - e(X))(T - e(X)) \right] &= 0 \\ \tau \mathbb{E} [ \underbrace{-1(T - e(X))^2}_{\psi_a} ] + \mathbb{E} [ \underbrace{(Y - \mu(X))(T - e(X))}_{\psi_b} ] &= 0 \\ \Rightarrow \tau = - \frac{\mathbb{E}[\psi_b(W; \eta)]}{\mathbb{E}[\psi_a(W; \eta)]} = \frac{\mathbb{E}[(Y - \mu(X))(T - e(X))]}{\mathbb{E}[(T - e(X))^2]} \end{align*} \]

Example AIPW-ATE

• Moment condition:

\[ \begin{align*} \mathbb{E} \left[ \mu(1, X) - \mu(0, X) + \frac{T(Y - \mu(1, X))}{e(X)} - \frac{(1 - T)(Y - \mu(0, X))}{1 - e(X)} - \tau_{\text{ATE}} \right] &= 0 \\ \tau_{\text{ATE}} \underbrace{(-1)}_{\psi_a} + \mathbb{E} \bigg[ \underbrace{\mu(1, X) - \mu(0, X) + \frac{T(Y - \mu(1, X))}{e(X)} - \frac{(1 - T)(Y - \mu(0, X))}{1 - e(X)}}_{\psi_b} \bigg] &= 0 \\ \Rightarrow \tau_{\text{ATE}} = -\frac{\mathbb{E}[\psi_b(W; \eta)]}{\mathbb{E}[\psi_a(W; \eta)]} = \mathbb{E} \left[ \mu(1, X) - \mu(0, X) + \frac{T(Y - \mu(1, X))}{e(X)} - \frac{(1 - T)(Y - \mu(0, X))}{1 - e(X)} \right] \end{align*} \]

Double ML Recipe

1. Find Neyman-orthogonal score for your target parameter:
   • can be constructed (see Chernozhukov et al. (2018), Section 2)
2. Predict nuisance parameters \(\hat{\eta}\) with cross-fitted high-quality ML.
3. Solve empirical moment condition to estimate the target parameter:
   • \(\theta = - \frac{\mathbb{E}[\psi_b(W, \eta)]}{\mathbb{E}[\psi_a(W, \eta)]}\)
4. Calculate standard error:
   • \(\hat{\sigma}^2 = \frac{N^{-1} \sum_{i} \psi(W_i; \hat{\theta}, \hat{\eta}_i)^2}{[N^{-1} \sum_{i} \psi_a(W_i; \hat{\eta}_i)]^2} \quad \Rightarrow \quad \text{se}(\hat{\theta}) = \sqrt{\frac{\hat{\sigma}^2}{N}}\)
   • To calculate t-values, confidence intervals, etc.
   • Can be motivated by the concept of influence functions.

Standard Errors in DML

• Influence functions:
  • \(\Psi(W; \theta, \eta) := - \mathbb{E} \left[ \frac{\partial \psi}{\partial \theta} \right]^{-1} \psi(W; \theta, \eta) = - \mathbb{E}[\psi_a(W; \eta)]^{-1} \psi(W; \theta, \eta)\)
  • Scaled version of the score with important characteristics:
    • \(\Psi(W_i; \theta, \eta_i)\) measures the influence of an estimator \(\theta\) to infinitesimal changes in the distribution, i.e. of each observation \(W_i\)
    • \(\mathbb{E}[\Psi(W; \theta, \eta)] = \mathbb{E}[ -\mathbb{E}[\psi_a(W; \eta)]^{-1} \psi(W; \theta, \eta)] = -\mathbb{E}[\psi_a(W; \eta)]^{-1} \underbrace{\mathbb{E}[\psi(W; \theta, \eta)]}_{=0} = 0\)

• Estimator distribution and influence function are closely linked:
  • \(\sqrt{N}(\hat{\theta} - \theta) = \frac{1}{\sqrt{N}} \sum_{i} \Psi(W_i; \theta, \eta_i) + o_p(1) \xrightarrow{d} N(0, \underbrace{\operatorname{Var}[\Psi(W; \theta, \eta)]}_{\sigma^2})\)
• Estimator variance (suppressing arguments for brevity):
  • \(\sigma^2 = \text{Var}[\Psi] = \mathbb{E}[\Psi^2] - \underbrace{\mathbb{E}[\Psi]^2}_{=0} = \mathbb{E}[\Psi^2] = \mathbb{E}[(\mathbb{E}[\psi_a]^{-1} \psi)^2] = \mathbb{E}[\psi_a]^{-2} \mathbb{E}[\psi^2] = \frac{\mathbb{E}[\psi^2]}{\mathbb{E}[\psi_a]^2}\)

Double ML Recipe: Example

• Assess the effect of 401(k) program participation on net financial assets of 9,915 households in the US in 1991.

# Load required packages
library(hdm)
library(mlr3)
library(mlr3learners)
library(tidyverse)

set.seed(1234) # for replicability

# Get data
data(pension)
pension <- pension[,c("net_tfa", "p401", "age", "db", "educ", "fsize", 
                   "hown", "inc", "male", "marr", "pira", "twoearn")]
# Outcome
Y = pension$net_tfa
# Treatment
T = pension$p401

# create folds
N = nrow(pension)
nfolds = 5
fold = sample(1:nfolds,N,replace=TRUE)


# initialize nuisance parameters
ehat = muhat = muhat0 = muhat1 = rep(NA,N)

# Define prediction model for the treatment/exposure
task_e <- as_task_classif(pension |> select(-net_tfa), target = "p401")
lrnr_e <- lrn("classif.ranger", predict_type = "prob")

# Define prediction model for the outcome
task_mu <- as_task_regr(pension |> select(-p401), target = "net_tfa")
lrnr_mu <- lrn("regr.ranger", predict_type = "response")

# cross fitting of nuisance parameters
for (i in 1:nfolds){
  # propensity score e(x)
  lrnr_e$train(task_e, row_ids = which(fold != i))
  ehat[which(fold == i)] <- lrnr_e$predict(task_e, row_ids = which(fold == i))$prob[, 2]
  
  # outcome mu(x)
  lrnr_mu$train(task_mu, row_ids = which(fold != i))
  muhat[which(fold == i)] <- lrnr_mu$predict(task_mu, row_ids = which(fold == i))$response
  
  # outcome mu(0,x)
  lrnr_mu$train(task_mu, row_ids = intersect(which(fold != i), which(pension$p401 == 0)))
  muhat0[which(fold == i)] <- lrnr_mu$predict(task_mu, row_ids = which(fold == i))$response
  
  # outcome mu(1,x)
  lrnr_mu$train(task_mu, row_ids = intersect(which(fold != i), which(pension$p401 == 1)))
  muhat1[which(fold == i)] <- lrnr_mu$predict(task_mu, row_ids = which(fold == i))$response
}

# DML-PLR
psi_a = -(T - ehat)^2
psi_b = (Y - muhat) * (T - ehat)
theta = -sum(psi_b) / sum(psi_a)
psi = theta * psi_a + psi_b
Psi = - psi / mean(psi_a)
sigma2 = var(Psi)
# sigma2 = mean(psi^2) / mean(psi_a)^2
se = sqrt(sigma2 / N)
t = theta / se
p = 2 * pt(abs(t),N,lower = FALSE)
result = c(round(theta, 2), round(se, 2), round(t, 2), round(p, 2))
result

# DML-AIPW
psi_a = rep(-1,length(Y))
psi_b = muhat1 - muhat0 + T * (Y - muhat1) / ehat - (1 - T) * (Y - muhat0) / (1-ehat)
theta = -sum(psi_b) / sum(psi_a)
psi = theta * psi_a + psi_b
Psi = - psi / mean(psi_a)
sigma2 = var(Psi)
# sigma2 = mean(psi^2) / mean(psi_a)^2
se = sqrt(sigma2 / N)
t = theta / se
p = 2 * pt(abs(t),N,lower = FALSE)
result = c(round(theta, 2), round(se, 2), round(t, 2), round(p, 2))
result

[1] 14082.91  1507.76     9.34     0.00

[1] 11285.34  1247.14     9.05     0.00

Thank you for your attention!
	startupengineer.io/authors/ihl christoph-ihl christophihl Ihluminate