(8) Difference-in-Differences

Causal Data Science for Business Analytics

Christoph Ihl

Hamburg University of Technology

Monday, 24. June 2024

Basic Model

Focus: ATT After Treatment

Unconfoundedness assumption \(\{Y(0), Y(1)\} \perp\!\!\!\perp T\) helps to identify the ATE: \(\tau_{\text{ATE}} = \mathbb{E}[Y_i|T_i=1] - \mathbb{E}[Y_i|T_i=0]\).
Average Treatment Effect on the Treated (ATT): \(\tau_{\text{ATT}} = \mathbb{E}[Y_i(1) - Y_i(0) | T_i=1]\)
- Weaker identification assumption suffices: \(Y(0) \perp\!\!\!\perp T|X\):

\[ \begin{align*} \tau_{\text{ATT}} = \mathbb{E}[Y_i(1) - Y_i(0) | T_i=1] &= \mathbb{E}[Y_i(1) | T_i=1] - \mathbb{E}[Y_i(0) | T_i=1] \\ &= \mathbb{E}[Y_i | T_i=1] - \mathbb{E}[Y_i(0) | T_i=1] \\ &= \mathbb{E}[Y_i | T_i=1] - \mathbb{E}[Y_i(0) | T_i=0] \\ &= \mathbb{E}[Y_i | T_i=1] - \mathbb{E}[Y_i | T_i=0] \end{align*} \]

Introducing time periods before and after treatment \(t=0,1\):
- \(\tau_{\text{DiD}} = \mathbb{E}[Y_{i,t=1}(1) - Y_{i,t=1}(0) | T_i=1]\)

Assumptions and Definition

In addition to SUTVA (consistency & no interference), two new assumptions:

Assumption (A.pt) “Parallel Trends”

\(\mathbb{E}[Y_{i,t=1}(0) - Y_{i,t=0}(0) | T_i=1] = \mathbb{E}[Y_{i,t=1}(0) - Y_{i,t=0}(0) | T_i=0]\).

Equivalent to unconfoundedness of the change (rather than potential outcomes themselves): \((Y_1(0)-Y_0(0)) \perp\!\!\!\perp T\).

Assumption (A.na) “No Anticipation”

\(\mathbb{E}[Y_{i,t=0}(1) - Y_{i,t=0}(0) | T_i=1] = 0 \quad\) or \(\quad Y_{i,t=0}(1) = Y_{i,t=0}(0)\)

Treatment has no effect on the treatment group before it is administered.

Definition “Difference-in-Differences ATT”

Given consistency, parallel trends, and no anticipation, the ATT is given by the difference between change in the treated group and change in the control group:

\(\tau_{\text{DiD}} = \mathbb{E}[Y_{i,t=1}(1) - Y_{i,t=1}(0) | T_i=1] = (\mathbb{E}[Y_{i,t=1} | T_i=1] - \mathbb{E}[Y_{i,t=0} | T_i=1]) - (\mathbb{E}[Y_{i,t=1} | T_i=0] - \mathbb{E}[Y_{i,t=0} | T_i=0])\).

Identification

Proof:

\[ \begin{aligned} \tau_{\text{DiD}} = \mathbb{E}[Y_{i,1}(1) - Y_{i,1}(0) | T_i=1] &\overset{\text{LIE}}{=} \mathbb{E}[Y_{i,1}(1) | T_i=1] - \mathbb{E}[Y_{i,1}(0) | T_i=1] \\ &= \mathbb{E}[Y_{i,1}(1) | T_i=1] {\color{#00C1D4}- \mathbb{E}[Y_{i,0}(0) | T_i=1]} - \mathbb{E}[Y_{i,1}(0) | T_i=1] {\color{#00C1D4}+ \mathbb{E}[Y_{i,0}(0) | T_i=1]} \\ & \overset{\text{(A.na)}}{=} \mathbb{E}[Y_{i,1}(1) | T_i=1] -\mathbb{E}[Y_{i,0}({\color{#00C1D4}1}) | T_i=1] - \mathbb{E}[Y_{i,1}(0) | T_i=1] + \mathbb{E}[Y_{i,0}(0) | T_i= 1] \\ & \overset{\text{(SUTVA)}}{=} {\color{#00C1D4}\mathbb{E}[Y_{i,1} | T_i=1]} - {\color{#00C1D4}\mathbb{E}[Y_{i,0} | T_i=1]} - {\color{#FF7E15}(\mathbb{E}[Y_{i,1}(0) - Y_{i,0}(0) | T_i= 1])} \\ & \overset{\text{(A.pt)}}{=} \mathbb{E}[Y_{i,1} | T_i=1] - \mathbb{E}[Y_{i,0} | T_i=1] - {\color{#00C1D4}(\mathbb{E}[Y_{i,1}(0) - Y_{i,0}(0) | T_i= 0])} \\ &\overset{\text{LIE}}{=} \mathbb{E}[Y_{i,1} | T_i=1] - \mathbb{E}[Y_{i,0} | T_i=1] - (\mathbb{E}[Y_{i,1}(0) | T_i=0] - \mathbb{E}[Y_{i,0}(0) | T_i=0]) \\ &\overset{\text{SUTVA}}{=} \underbrace{\mathbb{E}[Y_{i,1} | T_i=1] - \mathbb{E}[Y_{i,0} | T_i=1]}_{\text{change in the treated group}} - \underbrace{(\mathbb{E}[Y_{i,1} | T_i=0] - \mathbb{E}[Y_{i,0} | T_i=0])}_{\text{change in the control group}} \\ \end{aligned} \]

How DiD Estimation Works

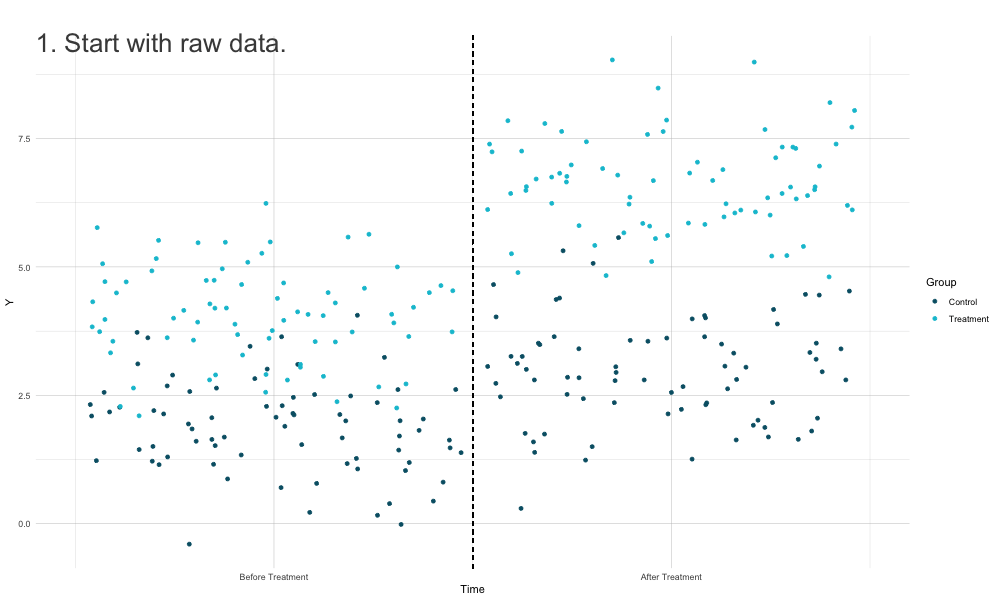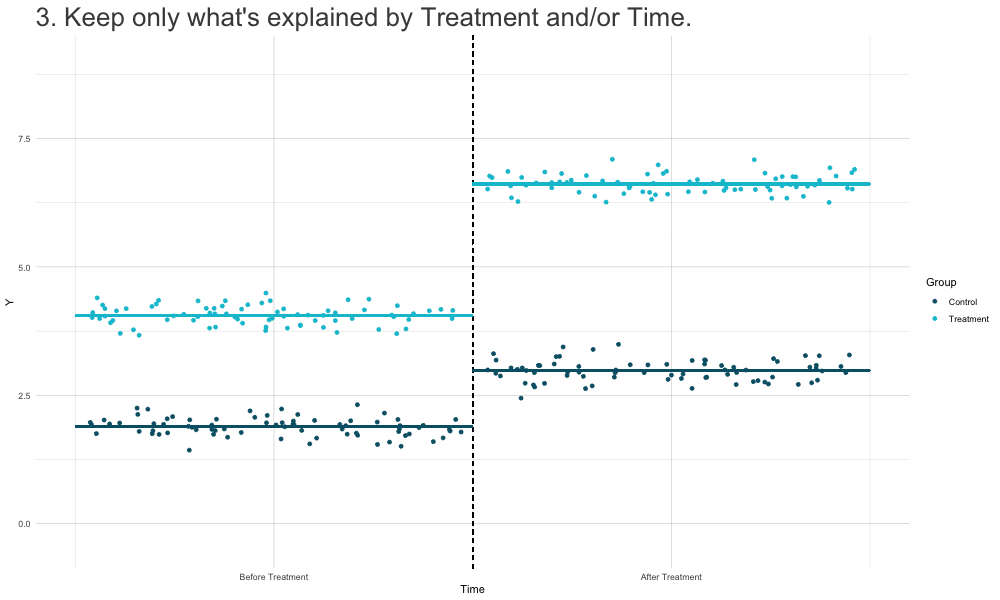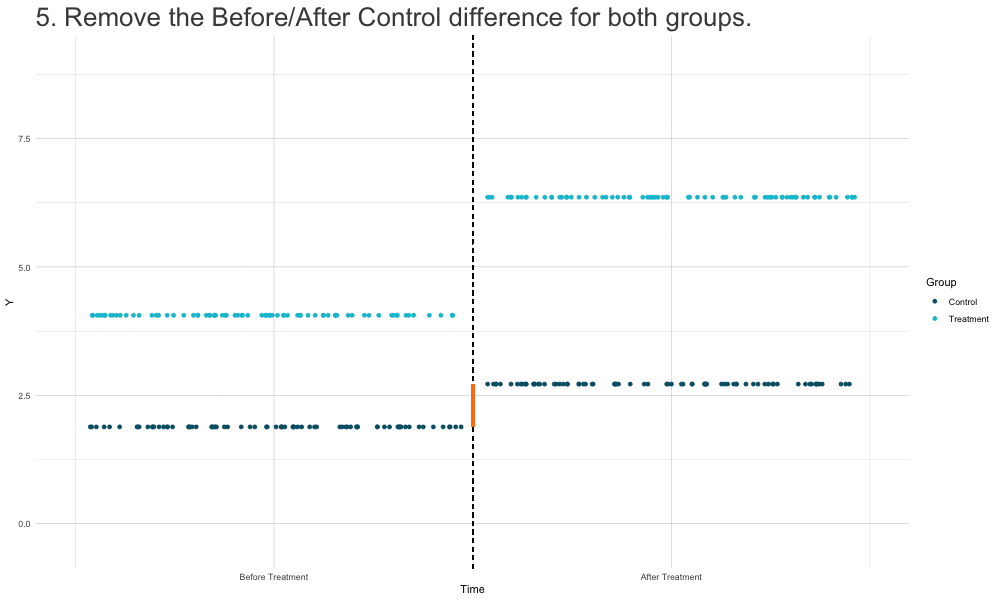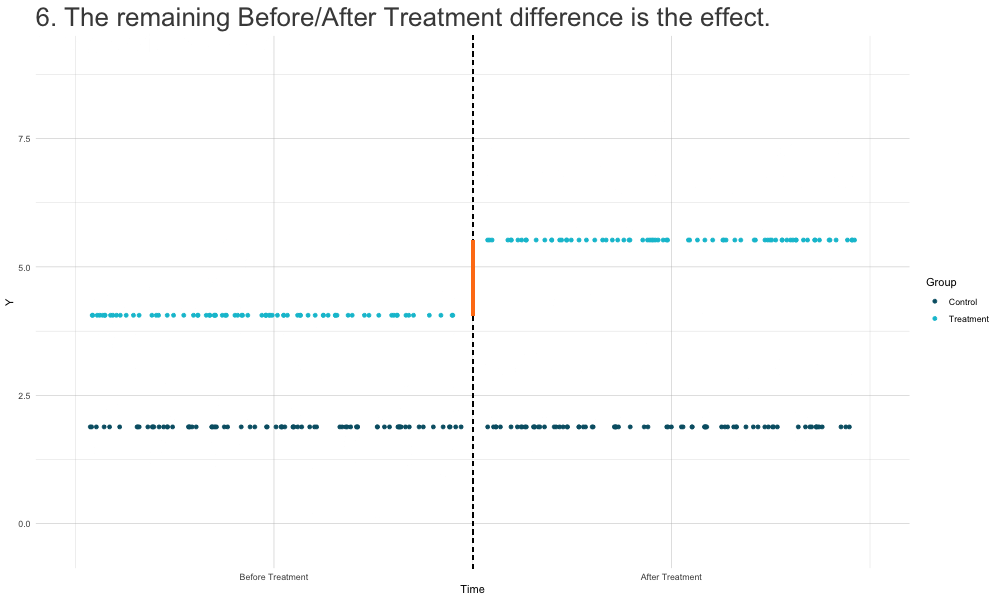
Diff-in-Diffs Regression

DiD estimator \(\tau_{\text{DiD}}\) can be obtained by two types of regressions:

Two-way fixed effects (TWFE) regression:
- \(Y_{i,t} = \alpha_i + \gamma_t + \tau_{\text{DiD}} (T_i \times t) + \epsilon_{i,t}\)
- Individual fixed effects \(\alpha_i\): capture time-invariant characteristics of individuals.
- Time fixed effects \(\gamma_t\): capture time-specific effects common to all individuals.
- Interaction between the treatment \(T_i\) and a time dummy \(t\): \(T_i \times t\).
- Works for panel data: i.e. same observations before and after treatment.

Regressing \(Y_i\) on the treatment \(T_i\), a time dummy \(t\) and their interaction \(T_i \times t\):
- \(Y_{i,t} = \alpha + \beta T_i + \gamma t + \tau_{\text{DiD}} (T_i \times t) + \epsilon_{i,t}\)
- Works for both panel data and repeated cross-sectionional data: i.e. different observations before and after treatment.

Diff-in-Diffs Regression

Graphical interpretation of \(Y_{i,t} = \alpha + \beta T_i + \gamma t + \tau_{\text{DiD}} (T_i \times t) + \epsilon_{i,t}\):
- \(\alpha = \mathbb{E}[Y_{i,0} | T_i=0]\) is the mean outcome of the nontreated at \(t=0\).
- \(\beta = \mathbb{E}[Y_{i,0} | T_i=1] - \mathbb{E}[Y_{i,0} | T_i=0]\) is the mean difference in outcomes across treatment groups at \(t=0\).
  - This selection bias should remain constant in \(t=1\).
- \(\gamma = \mathbb{E}[Y_{i,1} | T_i=0] - \mathbb{E}[Y_{i,0} | T_i=0]\) is the time trend in mean outcomes among the non-treated.
  - This trend should be the same (parallel) for the treated group.

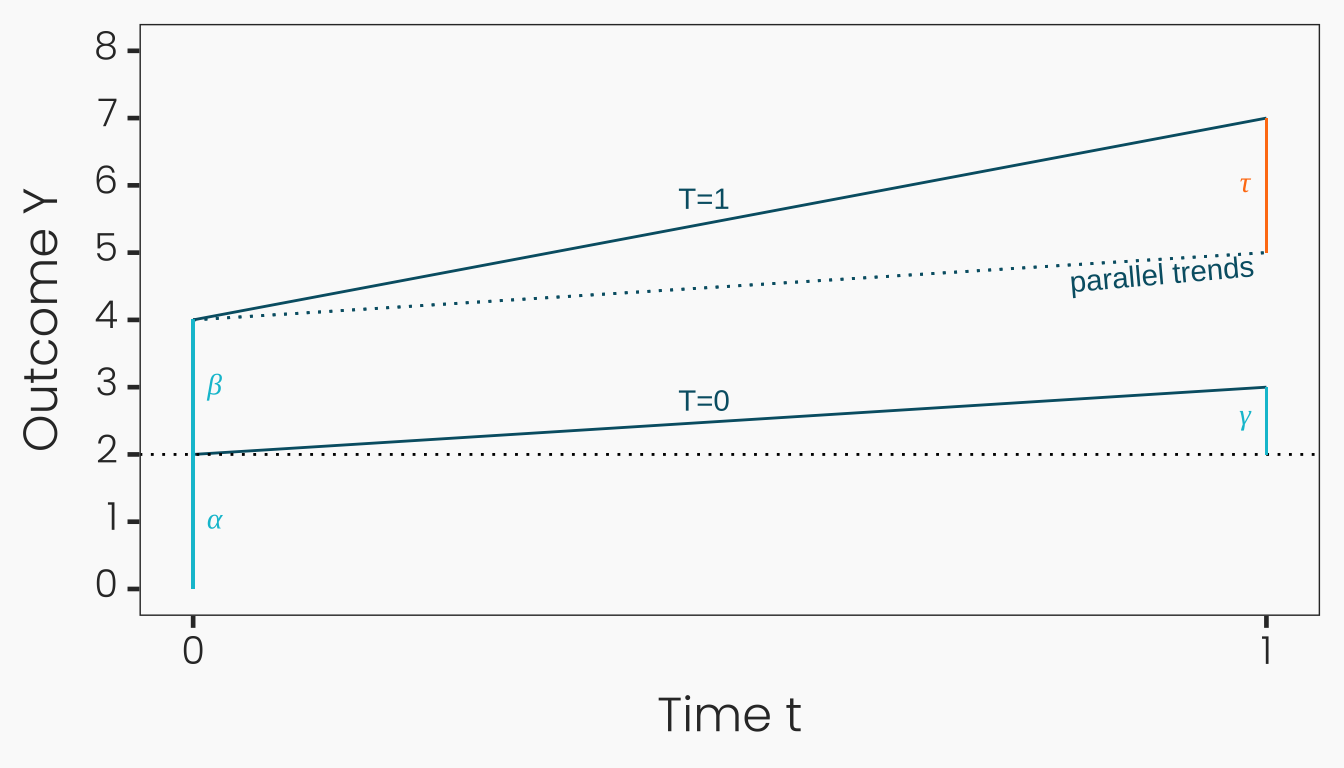
Alternative interpretation: \[ \begin{aligned} \tau_{\text{DiD}} = \underbrace{\mathbb{E}[Y_{i,1} | T_i=1] - \mathbb{E}[Y_{i,1} | T_i=0]}_{\text{difference in post-treatment}} \\ - \underbrace{(\mathbb{E}[Y_{i,0} | T_i=1] - \mathbb{E}[Y_{i,0} | T_i=0])}_{\text{difference in pre-treatment}} \end{aligned} \]

Basic DiD: Example

Repeated cross-sectional data: Assess house prices before and after a new highway is built. Repeated cross-section data of 179 houses in 1978 and 142 houses in 1981 in Kiel, Germany. Not the same houses over time.

library(wooldridge)  # load wooldridge package for data
library(fixest) # load fixest package for FE regression
data(kielmc)  # load kielmc data
attach(kielmc)   # attach data
kielmc$Y = kielmc$rprice  # define outcome
kielmc$T = kielmc$nearinc # define treatment group
kielmc$t = kielmc$y81     # define period dummy

feols(Y ~ T + t + T:t,    # eqivalent to lm(Y ~ T*t)
      data = kielmc, 
      vcov = vcov_cluster("cbd") # cluster st.error w.r.t. distance to center
)

OLS estimation, Dep. Var.: Y
Observations: 321
Standard-errors: Clustered (cbd) 
            Estimate Std. Error  t value   Pr(>|t|)    
(Intercept)  82517.2    3221.92 25.61117  < 2.2e-16 ***
T           -18824.4    7796.29 -2.41453 0.02146099 *  
t            18790.3    5154.86  3.64516 0.00090981 ***
T:t         -11863.9    6621.82 -1.79164 0.08236582 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 30,053.9   Adj. R2: 0.166131

Basic DiD: Example 2

Panel data: Assess the impact of participating in the U.S. National Supported Work (NSW) training program targeted to individuals with social and economic problems on their real earnings. Experimental vs. non-experimental control group.

library(tidyverse)
library(fixest)
library(haven) # to read Stata files
# 1. Experimental data
data <- haven::read_dta("https://raw.github.com/Mixtape-Sessions/Causal-Inference-2/master/Lab/Lalonde/lalonde_exp_panel.dta")
# ---- Difference-in-means - Averages
with(data, {y11 = mean(re[year == 78 & ever_treated == 1])
              y01 = mean(re[year == 78 & ever_treated == 0])
              dim = y11 - y01
              dim})

[1] 1794.342

# 2. Non-Experimental data
data <- haven::read_dta("https://raw.github.com/Mixtape-Sessions/Causal-Inference-2/master/Lab/Lalonde/lalonde_nonexp_panel.dta")
# ---- Difference-in-means - Averages
with(data, {y11 = mean(re[year == 78 & ever_treated == 1])
              y01 = mean(re[year == 78 & ever_treated == 0])
              dim = y11 - y01
              dim})

[1] -8497.516

# ---- Difference-in-Differences - Averages
with(data, {y00 = mean(re[year == 75 & ever_treated == 0])
              y01 = mean(re[year == 78 & ever_treated == 0])
              y10 = mean(re[year == 75 & ever_treated == 1])
              y11 = mean(re[year == 78 & ever_treated == 1])
              did = (y11 - y10) - (y01 - y00)
              did})

[1] 3621.232

data$post_treat = data$ever_treated * (data$year == 78)
# ---- Difference-in-Differences - Two-Way Fixed Effects Regression
feols(re ~ post_treat | id + year, 
        data = data |> filter(year %in% c(75, 78)),
        vcov = vcov_cluster(c("id", "year")))
# ---- Difference-in-Differences - Interactive Regression
feols(re ~ ever_treated + I(year == 78) + post_treat, 
        data = data |> filter(year %in% c(75, 78)),
        vcov = vcov_cluster(c("id", "year")))

OLS estimation, Dep. Var.: re
Observations: 32,354
Fixed-effects: id: 16,177,  year: 2
Standard-errors: Clustered (id & year) 
           Estimate Std. Error t value Pr(>|t|) 
post_treat  3621.23     609.84 5.93801  0.10621 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 3,859.0     Adj. R2: 0.670904
                Within R2: 0.002483

OLS estimation, Dep. Var.: re
Observations: 32,354
Standard-errors: Clustered (id & year) 
               Estimate Std. Error   t value  Pr(>|t|)    
(Intercept)    13650.80    51.4092  265.5324 0.0023975 ** 
ever_treated  -12118.75    99.1118 -122.2736 0.0052064 ** 
I(year == 78)   1195.86    21.2944   56.1583 0.0113350 *  
post_treat      3621.23    41.0534   88.2078 0.0072170 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 9,428.0   Adj. R2: 0.017819

Parallel Trends Conditional on Covariates

Parallel Trends Violations

Functional form misspecification:
- Sensitive to (even monotonic) transformations of the outcome (e.g. logarithm) unless the treatment is randomly assigned (Roth and Sant’Anna, 2021).

Compositional change with repeated cross-sections:
- Sample composition may have changed between the pre and post period in ways that are correlated with treatment (Sant’Anna and Xu, 2023).

Time-varying Confounding:
- Confounding in diff-in-diffs: covariate with time-varying effect on the outcome or a time-varying difference between groups.
- Time-invariant confounding: covariate differences between groups that are invariant over time, or covariate changes that are invariant across groups - cancel out due to differencing.
- Cross-sectional confounding in comparison: covariate associated with treatment & outcome.

Types of Confounding Covariates

Time-invariant covariate: \(X_{i}\)
- Does not change over time for an individual.
- Confounder if the means of the covariate are different in the two groups and it has a time-varying effect on the outcome.
Time-varying covariate: \(X_{i,t}\)
- Does change over time for an individual.
- Confounder if the covariate means evolve differently between the two groups or the covariate means start at different levels and evolve in parallel, and the covariate has a time-varying effect on the outcome.

Handling of Confounding Covariates

Most estimation approaches treat all covariates as time-invariant:
- Time-varying covariates are fixed at their pre-treatment value across all periods.
- Advantages: avoids time-varying confounders affected by treatment (mediators are “bad controls”) and helps to reduce the dimensionality of the problem.
- Disadvantage: no control for time trends in X independently of the treatment and thus PT violation remains.
Newer estimation approaches can handle time-varying covariates in more flexible ways (e.g. Caetano and Callaway, 2023):
- All covariates values from each period in each period (highest dimensionality).
- Covariates values from the current period and base period.
- Changes in covariate values from period to period.
- Average covariate values across time periods.

Conditional Parallel Trends

Parallel trend assumption often appear plausible only after controlling for observed covariates \(\mathbf{X_i}\):

Assumption (A.cpt) “Conditional Parallel Trends”

\(\mathbb{E}[Y_{i,t=1}(0) - Y_{i,t=0}(0) | T_i=1, \mathbf{X_i}] = \mathbb{E}[Y_{i,t=1}(0) - Y_{i,t=0}(0) | T_i=0, \mathbf{X_i}] \quad\) and

\(\mathbf{X_i}\) is not affected by \(T_i\): \(\quad \mathbf{X_i}(1) = \mathbf{X_i}(0) = \mathbf{X_i}\)

Conditional unconfoundedness of the change (rather than potential outcomes themselves): \((Y_1(0)-Y_0(0)) \perp\!\!\!\perp T \mid \mathbf{X_i}\).

Assumption (A.cna) “Conditionally No Anticipation”

\(\mathbb{E}[Y_{i,t=0}(1) - Y_{i,t=0}(0) | T_i=1, \mathbf{X_i}] = 0\)

Treatment has no effect on the treatment group before it is administered within the same strata of \(\mathbf{X_i}\).

Assumption (A.pos) “Positivity / Common Support / Overlap”

\(\Pr(T_i = 1 \mid \mathbf{X_i}) < 1 \space \text{and} \space \Pr(T_i = 1) > 0\).

For each treated unit with covariates \(\mathbf{X_i}\), there are at least some untreated units in the population with the same \(\mathbf{X_i}\).

ATT Conditional on Covariates: Identification

Given the conditional parallel trends assumption, no anticipation assumption, and overlap condition, the ATT conditional on \(\mathbf{X_i = x}\), \(\tau_{\text{DiD}}(\mathbf{x})\), can be identified for all \(\mathbf{x}\) with \(\Pr(T_i = 1 \mid \mathbf{X_i = x}) > 0\) as:

\[ \begin{aligned} \tau_{\text{DiD}}(\mathbf{x}) &= \mathbb{E}[Y_{i,1}(1) - Y_{i,1}(0) | T_i=1, \mathbf{X_i = x}] \\ &\overset{\text{LIE}}{=} \mathbb{E}[Y_{i,1}(1) | T_i=1, \mathbf{x}] - \mathbb{E}[Y_{i,1}(0) | T_i=1, \mathbf{x}] \\ &= \mathbb{E}[Y_{i,1}(1) | T_i=1, \mathbf{x}] {\color{#00C1D4}- \mathbb{E}[Y_{i,0}(0) | T_i=1, \mathbf{x}]} - \mathbb{E}[Y_{i,1}(0) | T_i=1, \mathbf{x}] {\color{#00C1D4}+ \mathbb{E}[Y_{i,0}(0) | T_i=1, \mathbf{x}]} \\ & \overset{\text{(A.cna)}}{=} \mathbb{E}[Y_{i,1}(1) | T_i=1, \mathbf{x}] -\mathbb{E}[Y_{i,0}({\color{#00C1D4}1}) | T_i=1, \mathbf{x}] - \mathbb{E}[Y_{i,1}(0) | T_i=1, \mathbf{x}] + \mathbb{E}[Y_{i,0}(0) | T_i= 1, \mathbf{x}] \\ & \overset{\text{(SUTVA)}}{=} {\color{#00C1D4}\mathbb{E}[Y_{i,1} | T_i=1, \mathbf{x}]} - {\color{#00C1D4}\mathbb{E}[Y_{i,0} | T_i=1, \mathbf{x}]} - {\color{#FF7E15}(\mathbb{E}[Y_{i,1}(0) - Y_{i,0}(0) | T_i= 1, \mathbf{x}])} \\ & \overset{\text{(A.cpt)}}{=} \mathbb{E}[Y_{i,1} | T_i=1, \mathbf{x}] - \mathbb{E}[Y_{i,0} | T_i=1, \mathbf{x}] - {\color{#00C1D4}(\mathbb{E}[Y_{i,1}(0) - Y_{i,0}(0) | T_i= 0, \mathbf{x}])} \\ &\overset{\text{LIE}}{=} \mathbb{E}[Y_{i,1} | T_i=1, \mathbf{x}] - \mathbb{E}[Y_{i,0} | T_i=1, \mathbf{x}] - (\mathbb{E}[Y_{i,1}(0) | T_i=0, \mathbf{x}] - \mathbb{E}[Y_{i,0}(0) | T_i=0, \mathbf{x}]) \\ &\overset{\text{SUTVA}}{=} \underbrace{\mathbb{E}[Y_{i,1} | T_i=1, \mathbf{x}] - \mathbb{E}[Y_{i,0} | T_i=1, \mathbf{x}]}_{\text{change for T=1 and X=x}} - \underbrace{(\mathbb{E}[Y_{i,1} | T_i=0, \mathbf{x}] - \mathbb{E}[Y_{i,0} | T_i=0, \mathbf{x}])}_{\text{change for T=0 and X=x}} \\ \end{aligned} \]

ATT Conditional on Covariates: Estimation

The unconditional ATT can then be identified by averaging \(\tau_{\text{DiD}}(\mathbf{x})\) over the distribution of \(X_i\) in the treated population.
Using the law of iterated expectations, we have:

\(\tau_{\text{DiD}} = \mathbb{E}[Y_{i,1}(1) - Y_{i,1}(0) | T_i=1] = \mathbb{E}_{\mathbf{X_i}}\left[ \underbrace{\mathbb{E}[Y_{i,1}(1) - Y_{i,1}(0) | T_i=1, \mathbf{X_i}]}_{\tau_{\text{DiD}}(\mathbf{X_i})} \mid T_i=1\right]\)

Four estimation procedures:
1. Two-Way Fixed Effects (TWFE) Regression
2. Outcome Regression Adjustment
3. Inverse Probability Weighting (IPW)
4. Doubly Robust Estimation

Two-Way Fixed Effects (TWFE) Regression

Augment TWFE specification with covariates (e.g. Zeldow and Hatfield, 2021):
- Time-invariant covariate with time-variant effect on outcome:
  - \(Y_{i,t} = \alpha_i + \gamma_t + \tau_{\text{DiD}} (T_i \times t) + \delta (X_i \times t) + \epsilon_{i,t}\)
- Time-variant covariate with time-invariant effect on outcome:
  - \(Y_{i,t} = \alpha_i + \gamma_t + \tau_{\text{DiD}} (T_i \times t) + \delta X_{it} + \epsilon_{i,t}\)
- Time-variant covariate with time-variant effect on outcome:
  - \(Y_{i,t} = \alpha_i + \gamma_t + \tau_{\text{DiD}} (T_i \times t) + \delta (X_{it} \times t) + \epsilon_{i,t}\)

Rather strong additional assumptions needed (e.g. Caetano and Callaway, 2023):
- Treatment effect is homogeneous across different values of X.
- Outcome is linear in X.
- Only controlling for covariate changes, not for levels.

TWFE Regression: Example

library(tidyverse)
library(fixest)
library(haven) # to read Stata files

data <- haven::read_dta("https://raw.github.com/Mixtape-Sessions/Causal-Inference-2/master/Lab/Lalonde/lalonde_nonexp_panel.dta")

data$post_treat = data$ever_treated * (data$year == 78)
data$post = as.integer(data$year == 78)

# ---- Difference-in-Differences - Two-Way Fixed Effects Regression
feols(
  re ~ post_treat + age:post + agesq:post + agecube:post + educ:post + educsq:post + marr:post + nodegree:post + black:post + hisp:post | id + year, 
  data = data |> filter(year %in% c(75, 78)),
  vcov = vcov_cluster(c("id", "year"))
)

OLS estimation, Dep. Var.: re
Observations: 32,354
Fixed-effects: id: 16,177,  year: 2
Standard-errors: Clustered (id & year) 
                  Estimate Std. Error   t value Pr(>|t|)    
post_treat     2450.964333 645.332739  3.797985 0.163900    
age:post      -1392.968721 188.627206 -7.384771 0.085686 .  
post:agesq       32.005450   5.576397  5.739450 0.109818    
post:agecube     -0.254779   0.052340 -4.867790 0.128988    
post:educ      -132.810162  95.337273 -1.393056 0.396361    
post:educsq      10.228897   3.957951  2.584392 0.235037    
post:marr      -578.337803 163.583509 -3.535429 0.175485    
post:nodegree   417.398327 193.694598  2.154930 0.276597    
post:black     -281.607046 205.559277 -1.369955 0.401418    
post:hisp      -126.167682 234.813629 -0.537310 0.686116    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 3,737.9     Adj. R2: 0.691052
                Within R2: 0.064074

Outcome Regression Adjustment

Regression Adjustment exploits the fact that under conditional parallel trends, strong overlap, and no anticipation the ATT can be written as (Heckman, Ichimura and Todd, 1997):

\[ \begin{aligned} \tau_{\text{DiD}} &= \mathbb{E}_{\mathbf{X_i}}\left[\space \underbrace{\mathbb{E}[Y_{i,1} - Y_{i,0} | T_i=1, \mathbf{X_i}] - \mathbb{E}[Y_{i,1} - Y_{i,0} | T_i=0, \mathbf{X_i}]}_{\tau_{\text{DiD}}(\mathbf{X_i})} \mid T_i=1\right] \\ &\overset{\text{LIE}}{=} \mathbb{E}[Y_{i,1} - Y_{i,0} | T_i=1] - \mathbb{E}_{\mathbf{X_i}}\left[\space \mathbb{E}[Y_{i,1} - Y_{i,0} | T_i=0, \mathbf{X_i}] \mid T_i=1\right]\\ &\overset{\text{LIE}}{=} \mathbb{E}[Y_{i,1} - Y_{i,0} | T_i=1] - \mathbb{E}_{\mathbf{X_i}}\left[\space \mathbb{E}[Y_{i,1} | T_i=0, \mathbf{X_i}] - \mathbb{E}[Y_{i,0} | T_i=0, \mathbf{X_i}] \mid T_i=1\right] \\ &:= \mathbb{E}[Y_{i,1} - Y_{i,0} | T_i=1] - \mathbb{E}_{\mathbf{X_i}}\left[\space \mu_{1}(0, \mathbf{X_i}) - \mu_{0}(0, \mathbf{X_i}) \mid T_i=1\right] \end{aligned} \]

Potential outcome evolution for the treatment group is imputed with a regression based only on X of the control group.
Sample version: \(\hat{\tau}_{\text{DiD}} =\frac{1}{N_1} \underset{i:T_i=1}{\sum} (( Y_{i,1} - Y_{i,0}) - (\hat{\mu}_{1}(0, \mathbf{X_i}) - \hat{\mu}_{0}(0, \mathbf{X_i})))\)
1. Estimate the conditional expectation of the outcome at time \(t\), \(\hat{\mu}_{t}(T_i = 0, \mathbf{X_i})\) among untreated units.
1. Create prediction for each treated unit using the covarite values \(X_i\) among the treated units.
1. Calculate difference between observed and predicted difference for each treated unit and average.

Outcome Regression Adjustment: Example

library(tidyverse)
library(DRDID)
library(haven) # to read Stata files

data <- haven::read_dta("https://raw.github.com/Mixtape-Sessions/Causal-Inference-2/master/Lab/Lalonde/lalonde_nonexp_panel.dta")

# ---- Difference-in-Differences - Double-robust
ordid(
  yname = "re", tname = "year", idname = "id", dname = "ever_treated", 
  xformla = ~ age + agesq + agecube + educ + educsq + marr + nodegree + black + hisp + re74 + u74,
  data = data |> filter(year == 75 | year == 78)
)

 Call:
ordid(yname = "re", tname = "year", idname = "id", dname = "ever_treated", 
    xformla = ~age + agesq + agecube + educ + educsq + marr + 
        nodegree + black + hisp + re74 + u74, data = filter(data, 
        year == 75 | year == 78))
------------------------------------------------------------------
 Outcome-Regression DID estimator for the ATT:
 
   ATT     Std. Error  t value    Pr(>|t|)  [95% Conf. Interval] 
1769.9984   643.0996    2.7523     0.0059    509.5233  3030.4736 
------------------------------------------------------------------
 Estimator based on panel data.
 Outcome regression est. method: OLS.
 Analytical standard error.
------------------------------------------------------------------
 See Sant'Anna and Zhao (2020) for details.

Outcome Regression with ML: Example

library(tidyverse)
library(mlr3)
library(mlr3learners)
library(haven) # to read Stata files

data <- haven::read_dta("https://raw.github.com/Mixtape-Sessions/Causal-Inference-2/master/Lab/Lalonde/lalonde_nonexp_panel.dta")
data <- data |> filter(year == 75 | year == 78) |> 
  select(-treat, -data_id) |>
  pivot_wider(names_from = year, values_from = re, names_prefix = "re_") |>
  mutate(re_diff = re_78 - re_75)
data_pred <- data |> select(re_diff, ever_treated, age, agesq, agecube, educ, educsq, 
                              marr, nodegree, black, hisp, re74, u74)

# Define prediction model for the outcome difference delta_mu
task_mu <- as_task_regr(data_pred |> select(-ever_treated), target = "re_diff")
lrnr_mu <- lrn("regr.ranger", predict_type = "response")
# learn outcome difference delta_mu among untreated
lrnr_mu$train(task_mu, row_ids = which(data$ever_treated == 0))
# predict outcome difference delta_mu among treated
delta_mu <- lrnr_mu$predict(task_mu, row_ids = which(data$ever_treated == 1))$response

Y1 <- data$re_78[data$ever_treated == 1]
Y0 <- data$re_75[data$ever_treated == 1]

mean( (Y1 - Y0) - delta_mu )

[1] 2188.271

Inverse Probability Weighting (IPW)

The IPW approach proposed by Abadie (2005):
- \(\tau_{\text{DiD}} = \mathbb{E}\left( \frac{ Y_{i,1} - Y_{i,0}}{P(T_i=1)} \frac{T_i - e(\mathbf{X_i})}{1-e(\mathbf{X_i})} \right)\)
- \(e(\mathbf{X_i}) = P[T_i = 1 | \mathbf{X_i}]\)
Sample version:
- \(\hat{\tau}_{\text{DiD}} = \frac{1}{N} \underset{i}{\sum} \left( \frac{ Y_{i,1} - Y_{i,0}}{P(T_i=1)} \frac{T_i - \hat{e}(\mathbf{X_i})}{1-\hat{e}(\mathbf{X_i})} \right)\)

Intuition: what happens when \(T_i=1\) and \(T_i=0\)?
- Weighting with the propensity only happens to the control group’s first differences – not the treatment groups!
- Why? Because it’s the \(Y_1(0)\) that is missing, not the \(Y_1(1)\).

IWP: Example

library(tidyverse)
library(DRDID)
library(haven) # to read Stata files

data <- haven::read_dta("https://raw.github.com/Mixtape-Sessions/Causal-Inference-2/master/Lab/Lalonde/lalonde_nonexp_panel.dta")

# ---- Difference-in-Differences - Double-robust
ipwdid(
  yname = "re", tname = "year", idname = "id", dname = "ever_treated", 
  xformla = ~ age + agesq + agecube + educ + educsq + marr + nodegree + black + hisp + re74 + u74,
  data = data |> filter(year == 75 | year == 78)
)

 Call:
ipwdid(yname = "re", tname = "year", idname = "id", dname = "ever_treated", 
    xformla = ~age + agesq + agecube + educ + educsq + marr + 
        nodegree + black + hisp + re74 + u74, data = filter(data, 
        year == 75 | year == 78))
------------------------------------------------------------------
 IPW DID estimator for the ATT:
 
   ATT     Std. Error  t value    Pr(>|t|)  [95% Conf. Interval] 
2048.1972   724.1233    2.8285     0.0047    628.9156  3467.4788 
------------------------------------------------------------------
 Estimator based on panel data.
 Hajek-type IPW estimator (weights sum up to 1).
 Propensity score est. method: maximum likelihood.
 Analytical standard error.
------------------------------------------------------------------
 See Sant'Anna and Zhao (2020) for details.

IWP with ML: Example

library(tidyverse)
library(mlr3)
library(mlr3learners)
library(haven) # to read Stata files
data <- haven::read_dta("https://raw.github.com/Mixtape-Sessions/Causal-Inference-2/master/Lab/Lalonde/lalonde_nonexp_panel.dta")
data <- data |> filter(year == 75 | year == 78) |> 
  select(-treat, -data_id) |>
  pivot_wider(names_from = year, values_from = re, names_prefix = "re_")
data_pred <- data |> select(re_78, re_75, ever_treated, age, agesq, agecube, educ, educsq, 
                            marr, nodegree, black, hisp, re74, u74)

# Define prediction model for the propensity score e
task_e <- as_task_classif(data_pred |> select(-re_78, -re_75), target = "ever_treated")
lrnr_e <- lrn("classif.ranger", predict_type = "prob")
# Learn propensity score e among all observations
lrnr_e$train(task_e)
# Predict propensity score ehat
ehat <- lrnr_e$predict(task_e)$prob[, 2]

# Calculate the ATT
T <- data$ever_treated
P <- mean(data$ever_treated)
Y1 <- data$re_78
Y0 <- data$re_75

mean( (Y1-Y0)/P * (T - ehat)/(1-ehat) )

[1] 2906.464

Doubly Robust Estimation

Outcome regression and IPW approaches can also be combined in the context of Diff-in-Diffs to form “doubly-robust” (DR) methods that are valid if either the outcome model or the propensity score model is correctly specified (Sant’Anna and Zhao, 2020):
- \(\tau_{\text{DiD}} = \mathbb{E}\left( (Y_{i,1} - Y_{i,0} - (\mu_{1}(0, \mathbf{X_i}) - \mu_{0}(0, \mathbf{X_i}))) \left(\frac{T_i - e(\mathbf{X_i})}{P(T_i)(1-e(\mathbf{X_i}))}\right) \right)\)
Sample version:
- \(\hat{\tau}_{\text{DiD}} = \frac{1}{N} \underset{i}{\sum} \left( (Y_{i,1} - Y_{i,0} - (\hat{\mu}_{1}(0, \mathbf{X_i}) - \hat{\mu}_{0}(0, \mathbf{X_i}))) \left(\frac{T_i - \hat{e}(\mathbf{X_i})}{P(T_i)(1-\hat{e}(\mathbf{X_i}))}\right) \right)\)
Double machine learning for difference-in-differences models (Chang, 2020).

Doubly Robust Estimation: Example

library(tidyverse)
library(DRDID)
library(haven) # to read Stata files

data <- haven::read_dta("https://raw.github.com/Mixtape-Sessions/Causal-Inference-2/master/Lab/Lalonde/lalonde_nonexp_panel.dta")

# ---- Difference-in-Differences - Double-robust
drdid(
  yname = "re", tname = "year", idname = "id", dname = "ever_treated", 
  xformla = ~ age + agesq + agecube + educ + educsq + marr + nodegree + black + hisp + re74 + u74,
  data = data |> filter(year == 75 | year == 78)
)

 Call:
drdid(yname = "re", tname = "year", idname = "id", dname = "ever_treated", 
    xformla = ~age + agesq + agecube + educ + educsq + marr + 
        nodegree + black + hisp + re74 + u74, data = filter(data, 
        year == 75 | year == 78))
------------------------------------------------------------------
 Further improved locally efficient DR DID estimator for the ATT:
 
   ATT     Std. Error  t value    Pr(>|t|)  [95% Conf. Interval] 
2032.9217   707.4779    2.8735     0.0041    646.265   3419.5784 
------------------------------------------------------------------
 Estimator based on panel data.
 Outcome regression est. method: weighted least squares.
 Propensity score est. method: inverse prob. tilting.
 Analytical standard error.
------------------------------------------------------------------
 See Sant'Anna and Zhao (2020) for details.

Doubly Robust Estimation with ML: Example

library(tidyverse)
library(mlr3)
library(mlr3learners)
library(haven) # to read Stata files

data <- haven::read_dta("https://raw.github.com/Mixtape-Sessions/Causal-Inference-2/master/Lab/Lalonde/lalonde_nonexp_panel.dta")
data <- data |> filter(year == 75 | year == 78) |> 
  select(-treat, -data_id) |>
  pivot_wider(names_from = year, values_from = re, names_prefix = "re_") |>
  mutate(re_diff = re_78 - re_75)
data_pred <- data |> select(re_diff, ever_treated, age, agesq, agecube, educ, educsq, 
                            marr, nodegree, black, hisp, re74, u74)

# Define prediction model for the propensity score e
task_e <- as_task_classif(data_pred |> select(-re_diff), target = "ever_treated")
lrnr_e <- lrn("classif.ranger", predict_type = "prob")
# Learn propensity score e among all observations
lrnr_e$train(task_e)
# Predict propensity score ehat
ehat <- lrnr_e$predict(task_e)$prob[, 2]

# Define prediction model for the outcome difference delta_mu
task_mu <- as_task_regr(data_pred |> select(-ever_treated), target = "re_diff")
lrnr_mu <- lrn("regr.ranger", predict_type = "response")
# learn outcome difference delta_mu among untreated
lrnr_mu$train(task_mu, row_ids = which(data$ever_treated == 0))
# predict outcome difference delta_mu among all observations
delta_mu <- lrnr_mu$predict(task_mu)$response

# Calculate the ATT
T <- data$ever_treated
P <- mean(data$ever_treated)
Y1 <- data$re_78
Y0 <- data$re_75

mean( ((Y1-Y0) - delta_mu) * (T - ehat)/(P*(1-ehat)) )

[1] 2283.593

Staggered treatment Timing

Staggered Timing

Remember basic DiD model:
- Two periods and a common treatment date.
- Identification from parallel trends and no anticipation.
Active recent literature has focused on relaxing the first assumption:
- What if there are multiple periods and units adopt treatment at different times?
- Maintaining parallel trends and no anticipation assumptions.

Notation:
- Panel of observations \(i\) and time periods \(t = 1 ... T_t\).
- Units adopt a binary treatment at different dates \(G_i \in (1, ..., T_t) \cup \infty\).
  - where \(G_i = \infty\) means never-treated.
- Potential outcomes \(Y_{it}(g)\) depend on time (\(t\)) and time you were first treated (\(g\)).

Literature is now starting to consider cases with continuous treatment & treatments that turn on/off.
- still developing; for a review see de Chaisemartin and D’Haultfœuille (2023).

Extending the Identifying Assumptions

Key identifying assumptions from the canonical model are extended in a natural way:

Assumption (A.stpt) “Parallel Trends”

\(\mathbb{E}[Y_{i,t}(\infty) - Y_{i,t-1}(\infty) | G_i=g] = \mathbb{E}[Y_{i,t-1}(\infty) - Y_{i,t}(\infty) | G_i=g'] \quad \forall g, g', t\).

Intuitively, says that if treatment hadn’t happened, all “adoption cohorts” would have parallel average outcomes in all periods. (Note: could impose slightly weaker versions, e.g. only require PT post-treatment).

Assumption (A.stna) “No Anticipation”

\(\mathbb{E}[Y_{i,t}(g) - Y_{i,t}(\infty) | T_i=1] = 0 \quad\) or \(\quad Y_{i,t}(g) = Y_{i,t}(\infty) \quad \forall t < g\)

Treatment has no effect on the treatment group before it is administered.

TWFE Regression with Staggered Timing

Suppose we extend Two-way fixed effects (TWFE) regression to staggered treatment timing:
- \(Y_{i,t} = \alpha_i + \gamma_t + \beta D_{it} + \epsilon_{i,t}\)
- where \(D_{it} = 1[t \geq G_i]\) is an indicator for whether the unit has been treated by time \(t\).

Given no anticipation and parallel trends across all adoption cohorts:
- if treatment effect is constant across time and units, \(Y_{it}(g) - Y_{it}(\infty) \equiv \tau\), identification possible: \(\tau = \beta\).
- if treatment effect is heterogeneous, i.e. depends on time since treatement, \(Y_{it}(t-r) - Y_{it}(\infty) \equiv \tau_r\), then identification fails, because some \(\tau_{r}\)’s may get negative weights.

Reason:
- Clean comparisons: DiD’s between treated and not-yet-treated units.
- Forbidden comparisons: DiD’s between already-treated units (who began treatment at different times).
  - can lead to negative weights, if treatment effects in the already treated “control group” change over time.

Forbidden Comparisons in TWFE: Intuition

1. Suppose two period model with two groups: always treated (in both periods) & switchers (treated only in period 2).
- With two periods, \(Y_{i,t} = \alpha_i + \gamma_t + \beta D_{it} + \epsilon_{i,t}\) is the same as \(\Delta Y_{i} = \alpha + \beta \Delta D_{i} + u_i\) (by first-differencing).
- \(\Delta D_{i} = 1\) for switchers and \(0\) for the control group of always treated, thus:
- \(\hat{\beta} = \left( \overline{Y}_{\text{switchers}, 2} - \overline{Y}_{\text{switchers}, 1} \right) - \left( \overline{Y}_{\text{AT}, 2} - \overline{Y}_{\text{AT}, 1} \right)\)
- Problem: if treatment effect for always-treated grows over time, \(\hat{\beta}\) can get negative weights.

1. Frisch-Waugh-Lovell theorem says that we can obtain \(\beta\) in \(Y_{i,t} = \alpha_i + \gamma_t + \beta D_{it} + \epsilon_{i,t}\) in two steps:
- 1. Regress \(D_{i,t}\) on fixed effects (in a linear probability model - LPM): \(D_{i,t} = \tilde{\alpha}_i + \tilde{\gamma}_t + \tilde{\epsilon}_{i,t}\).
- 1. Regress \(Y_{i,t}\) on \(D_{i,t} - \hat{D}_{i,t}\), thus: \(\beta = \frac{\mathbb{E}(Y_{i,t}(D_{i,t} - \hat{D}_{i,t}))}{Var(D_{i,t} - \hat{D}_{i,t})}\).
- However, LPMs can predict \(\hat{D}_{i,t} > 1\), and \(Y_{it}\) can get negative weight.

1. Even if weights are non-negative (i.e. individual \(\tau_i\)’s are constant - no dynamics), \(\beta\) might still be biased:
- \(\beta = \sum_{i=1}^{N} \sum_{t=1}^{T_t} w_{it} \beta_{it}\): \(w_{it}\) is inversely proportional to the variance of \(\beta_{it}\).
  - Proportional to available information for \(i\), i.e. the number of observations pre and post treatment.
- But are individuals in the middle of the panel also the most representative of the population?

Dynamic TWFE Regression with Staggered Timing

Sun and Abraham (2021) show that similar issues arise with dynamic TWFE (“event study”) specifications:
- \(Y_{i,t} = \alpha_i + \gamma_t + \sum_{k \neq 0} \beta_k D_{it}^k + \epsilon_{i,t}\)
- where \(D_{it}^k = 1[t - G_i = k]\) are leading and lagging “event time” dummies.

This dynamic specification yields a sensible causal estimand when there is heterogeneity only in time since treatment.
However, if there is heterogeneity in dynamic treatment effects also across adoption cohorts, then:
- Like for static TWFE, \(\beta_k\) may put negative weight on treatment effects after k periods for some units.
- Furthermore, \(\beta_k\) may be “contaminated” by treatment effects at different leads and lags \(k' \neq k\).

Thus, interpreting \(\beta_k\) as estimates …
- of the dynamic effects of treatment (\(k>0\)) may be misleading.
- for pre-trends tests (\(k<0\)) may also be misleading.
  - We will return to pre-trends tests later.

New DiD-Estimators for Staggered Timing

Estimators based on clean aggregated comparisons:
- Callaway and Sant’Anna (2021): R package ‘did’ (Focus)
- Sun and Abraham (2021): R package ‘fixest’
Estimators based on imputation:
- Gardner, Thakral, Tô, and Yap (2024): R package ‘did2s’ (Focus)
- Borusyak, Jaravel, Spiess (2024): R package ‘did_imputation’
- Wooldridge (2021): R package ‘etwfe’
Estimators that can handle non-absorbing and/or non-binary treatments:
- de Chaisemartin and D’Haultfoeuille (2020): R package ‘DIDmultiplegt’
Estimators based on stacking:
- Cengiz, Dube, Lindner, and Zipperer (2019)
- Dube, Girardi, Jorda, and Taylor (2023)

Estimator by Callaway & Sant’Anna (2021)

Callaway & Sant’Anna (2021) define the group-time-specific treatment effect on the treated:
- \(\tau(g, t) = \mathbb{E}[Y_{i,t}(g) - Y_{i,t}(\infty) | G_i=g]\), with \(t \geq g\).
- ATT in period \(t\) for units first treated in period \(g\).

Under PT and No Anticipation, it can be identified as:
- \(\tau(g, t) = \underbrace{\mathbb{E}[Y_{i,t} - Y_{i,g-1} | G_i=g]}_{\text{change for cohort g}} - \underbrace{\mathbb{E}[Y_{i,t} - Y_{i,g-1} | G_i = \infty]}_{\text{change for never-treated}}\)
- Similar to the basic model, this is a two-group two-period comparison.
  - Similar identification proof (next).
- Differences:
  - 1. Period \(g-1\) is pre-treatment period (right before cohort g becomes treated).
  - 1. More flexibility in terms of comparison group: (a) never-treated, (b) not-yet-treated, (c) not-yet-but-eventually-treated, (d) last-to-be-treated.

Sample version of \(\tau(g, t)\):
- \(\hat{\tau}(g, t) = \frac{1}{N_{g}} \sum_{i=1}^{N_g} \left( Y_{i,t} - Y_{i,g-1} \right) 1[G_i = g] - \frac{1}{N_{\infty}} \sum_{i=1}^{N_{\infty}} \left( Y_{i,t} - Y_{i,g-1} \right) 1[G_i = \infty]\)

Callaway & Sant’Anna (2021): Proof

Start with identification result and work backwards:
- \(\mathbb{E}[Y_{i,t} - Y_{i,g-1} | G_i=g] - \mathbb{E}[Y_{i,t} - Y_{i,g-1} | G_i = \infty]\)
Apply definition of Potential Outcomes:
- \(\mathbb{E}[Y_{i,t}(g) - Y_{i,g-1}(g) | G_i=g] - \mathbb{E}[Y_{i,t}(\infty) - Y_{i,g-1}(\infty) | G_i = \infty]\)
Use No Anticipation to substitute \(Y_{i,g-1}(\infty)\) for \(Y_{i,g-1}(g)\):
- \(\mathbb{E}[Y_{i,t}(g) - Y_{i,g-1}(\infty) | G_i=g] - \mathbb{E}[Y_{i,t}(\infty) - Y_{i,g-1}(\infty) | G_i = \infty]\)
Add and subtract \(\mathbb{E}[Y_{i,t}(\infty) | G_i=g]\):
- \(\mathbb{E}[Y_{i,t}(g) - Y_{i,g-1}(\infty) | G_i=g] - \mathbb{E}[Y_{i,t}(\infty) - Y_{i,g-1}(\infty) | G_i = \infty] + \mathbb{E}[Y_{i,t}(\infty) | G_i=g] - \mathbb{E}[Y_{i,t}(\infty) | G_i=g]\)
Rearrange terms:
- \(\mathbb{E}[Y_{i,t}(g) - Y_{i,t}(\infty) | G_i=g] + \underbrace{\mathbb{E}[Y_{i,t}(\infty) - Y_{i,g-1}(\infty) | G_i=g] - \mathbb{E}[Y_{i,t}(\infty) - Y_{i,g-1}(\infty) | G_i = \infty]}_{=0}\)
QED:
- \(\tau(g, t) = \mathbb{E}[Y_{i,t}(g) - Y_{i,t}(\infty) | G_i=g]\)

Callaway & Sant’Anna (2021): Aggregation

If have a large number of observations and relatively few groups/periods, can report \(\hat{\tau}(g, t)\)’s directly.
If there are many groups/periods, the \(\hat{\tau}(g, t)\)’s may be very imprecisely estimated and/or too numerous to report.
In these cases, it is often desirable to report meaningful averages of the \(\hat{\tau}(g, t)\)’s.
Four aggregation schemes:
- Simple:
  - Computes a single weighted average of all group-time average treatment effects with weights proportional to group size.
- Dynamic:
  - Computes event-study parameters which average the \(\hat{\tau}(g, t)\)’s at a particular lag since (or lengths of exposure to) the treatment.
  - Can also be constructed for k < 0 to estimate “pre-trends”.
- Group:
  - Computes group averages which average the \(\hat{\tau}(g, t)\)’s for a particular cohort treated a \(g\).
- Calendar:
  - Computes “calendar averages” which average the \(\hat{\tau}(g, t)\)’s for a particular calendar time (year).

Callaway & Sant’Anna (2021): Further Variants

Anticipation:
- In many applications, units may observe that an intervention is about to occur, so that they change their behaviors before the intervention is actually implemented.
- Straightforward adaptation: if there is one period of anticipation, set the base period to \(g−2\) rather than \(g−1\), so that:
  - \(\tau(g, t) = \mathbb{E}[Y_{i,t} - Y_{i,g-2} | G_i=g] - \mathbb{E}[Y_{i,t} - Y_{i,g-2} | G_i = \infty]\)

Covariates:
- Staggered timing estimator can also be extended to include covariates:
  - 1. Conditional outcome regression.
  - 1. Inverse Probability Weighting.
  - 1. Doubly Robust Estimation.

Callaway & Sant’Anna (2021): Example

Assess the impact of job displacement (i.e. losing job w/o own fault, e.g. mass layoff) on income of 1,298 individuals.

library(did) # Load the 'did' package
library(fixest) # Load the 'fixest' package
temp_file <- tempfile(fileext = ".RData") # Define a temporary file path to save the downloaded file
# Download the file from Dropbox
download.file("https://www.dropbox.com/scl/fi/wnp1hrkz00izr72h6ua1t/job_displacement_data.RData?rlkey=nr15rrbv1ev8ra1kzfa1knux2&dl=1", temp_file, mode = "wb")
load(temp_file) # Load the RData file into the R session
rm(temp_file) # Optionally, remove the temporary file


# Check the structure of the loaded data
head(job_displacement_data)

# run TWFE
fixest::feols(income ~ i(year >= group) | id + year,
              data=job_displacement_data,
              cluster=c("id", "year"))

# A tibble: 6 × 7
       id  year group income female white occ_score
    <dbl> <dbl> <dbl>  <dbl>  <dbl> <dbl>     <dbl>
1 7900002  1984     0  31130      1     1         4
2 7900002  1985     0  32200      1     1         3
3 7900002  1986     0  35520      1     1         4
4 7900002  1987     0  43600      1     1         4
5 7900002  1988     0  39900      1     1         4
6 7900002  1990     0  38200      1     1         4

OLS estimation, Dep. Var.: income
Observations: 11,682
Fixed-effects: id: 1,298,  year: 9
Standard-errors: Clustered (id & year) 
                    Estimate Std. Error  t value Pr(>|t|)    
year >= group::TRUE -6455.36    2041.49 -3.16208 0.013353 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 14,824.0     Adj. R2: 0.674268
                 Within R2: 0.002425

Callaway & Sant’Anna (2021): Example cont’d

Assess the impact of job displacement (i.e. losing job w/o own fault, e.g. mass layoff) on income of 1,298 individuals.

# run command to obtain 64 (8 years * 8 groups) Tau(t,g)'s
result <- att_gt(
  yname = "income",
  tname = "year",
  idname = "id",
  gname = "group",
  xformla = ~ female + white + occ_score, #  ~ 1
  data = job_displacement_data,
  allow_unbalanced_panel = TRUE,
  control_group = "nevertreated", # "notyettreated"
  anticipation = 0,
  clustervars = "id",
  est_method = "dr", # "reg", "ipw"
  )

# aggregate results over time since treatment
result_es <- aggte(result, type="dynamic")
ggdid(result_es)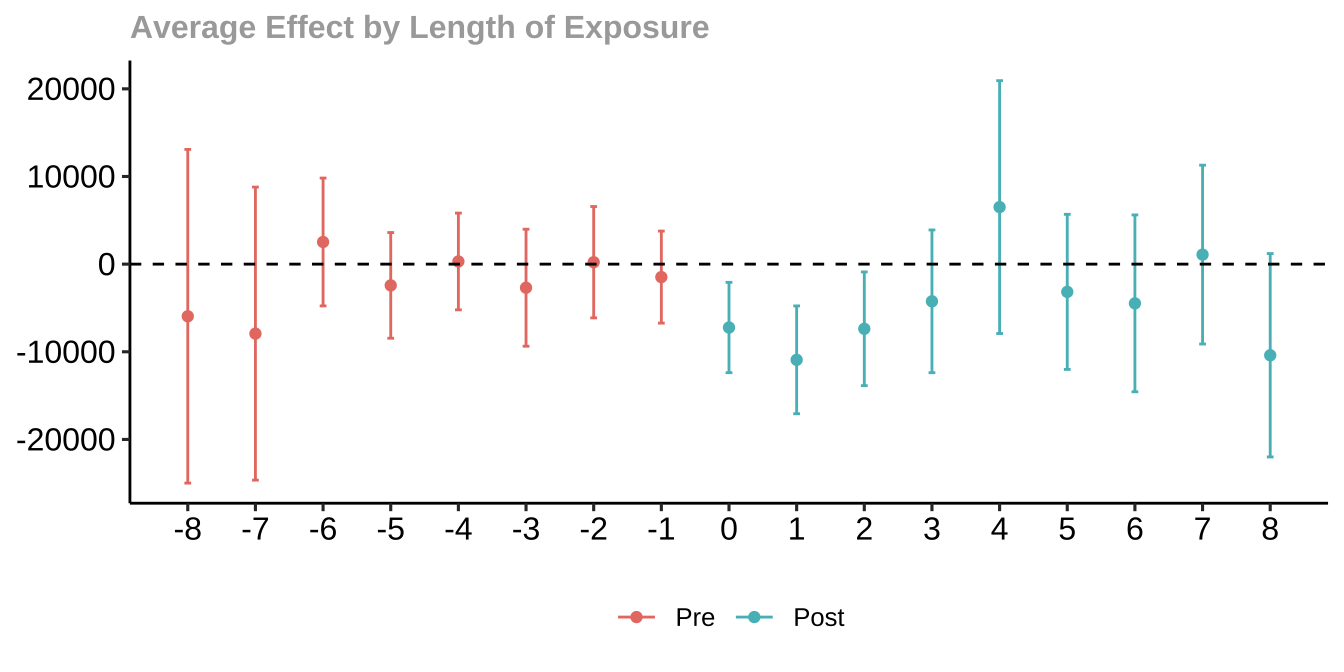

# aggregate results over groups and overall
result_overall <- aggte(result, type="group")
summary(result_overall)


Call:
aggte(MP = result, type = "group")

Reference: Callaway, Brantly and Pedro H.C. Sant'Anna.  "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015> 


Overall summary of ATT's based on group/cohort aggregation:  
       ATT    Std. Error     [ 95%  Conf. Int.]  
 -6290.805      1664.296  -9552.766   -3028.844 *


Group Effects:
 Group    Estimate Std. Error [95% Simult.  Conf. Band]  
  1985  -9152.7025   2998.059    -15874.750   -2430.655 *
  1986  -1863.3794   5769.769    -14799.971   11073.212  
  1987    816.6743   6509.247    -13777.925   15411.274  
  1988   6797.5169   4136.877     -2477.913   16072.947  
  1990 -13962.6186   3847.891    -22590.104   -5335.134 *
  1991  -7107.5120   5033.109    -18392.415    4177.391  
  1992 -10570.4752   8649.169    -29963.066    8822.115  
  1993 -24680.0159   5672.560    -37398.653  -11961.379 *
---
Signif. codes: `*' confidence band does not cover 0

Control Group:  Never Treated,  Anticipation Periods:  0
Estimation Method:  Doubly Robust

Imputation-based Estimation: Procedure

Recall the TWFE specification (with covariates) with the (heterogeneous) \(\tau_{it}\) if PT assumption holds:
- \(Y_{i,t} = \alpha_i + \gamma_t + \tau_{it} D_{it} + \delta X_{it} + \epsilon_{i,t}\)
- where \(D_{it} = T_i \times t\) and \(\mathbb{E}[\epsilon_{i,t} | \{D_{it}, X_{it}\}_{t=1}^{T_t}] = 0\)

If we have some \(t\) where \(D_{it}= 0\) for all \(i\) (e.g. pre-treatment period observations), two-stage procedure:
- 1. Using all observations with \(D_{it}= 0\), regress \(Y_{i,t}\) on the fixed effect \(\alpha_i\) and \(\gamma_t\) as well as on the covariates \(X_{it}\):
  - \(Y_{i,t}(0) = \alpha_i + \gamma_t + \delta X_{it} + \epsilon_{i,t}\).
  - Obtain \(\hat{Y}_{i,t}(0) = \hat{\alpha}_i + \hat{\gamma}_t + \hat{\delta} X_{it}\).
- 1. Regress adjusted outcomes \(Y_{i,t} - \hat{Y}_{i,t}(0)\) on \(D_{it}\) to obtain \(\hat{\tau}_{it}\):
  - \((Y_{i,t} - \hat{Y}_{i,t}(0)) = \alpha_0 + \tau_{it} D_{it} + \epsilon_{i,t}\).

With events studies of the form \(Y_{i,t} = \alpha_i + \gamma_t + \sum_{k \neq 0} \tau_{it}^k D_{it}^k + \delta X_{it} + \epsilon_{i,t}\):
- 1st stage remains the same.
- 2nd stage: Regress adjusted outcomes \(Y_{i,t} - \hat{Y}_{i,t}(0)\) on event dummies \(D_{it}^k\) to obtain \(\hat{\tau}_{it}^k\):
  - \((Y_{i,t} - \hat{Y}_{i,t}(0)) = \alpha_0 + \sum_{k \neq 0} \tau_{it}^k D_{it}^k + \epsilon_{i,t}\).

Imputation-based Estimation: Comparison

Approaches of Gardner, Thakral, Tô, and Yap (2024) and Borusyak, Jaravel, Spiess (2024) are very similar:
- Same point estimates, but differ in deriving standard errors.

Key difference to C&S (2021) is the trade-off between efficiency and strength of identifying assumption:
- Plus: averaging over multiple pre-treatment periods (instead of one) can increase precision.
- Minus: parallel trends need to hold for all groups and time periods (instead of only post-treatment parallel trends).

Imputation-based Estimation: Example

Assess the impact of job displacement (i.e. losing job w/o own fault, e.g. mass layoff) on income of 1,298 individuals.

library(did2s) # Load the 'did' package
library(tidyverse) # Load the 'tidyverse' package
temp_file <- tempfile(fileext = ".RData") # Define a temporary file path to save the downloaded file
# Download the file from Dropbox
download.file("https://www.dropbox.com/scl/fi/wnp1hrkz00izr72h6ua1t/job_displacement_data.RData?rlkey=nr15rrbv1ev8ra1kzfa1knux2&dl=1", temp_file, mode = "wb")
load(temp_file) # Load the RData file into the R session
rm(temp_file) # Optionally, remove the temporary file

job_displacement_data <- job_displacement_data |> 
  # create time-variant treatment indicator D_it
  mutate(d_it = case_when(
    group == 0 ~ 0,
    year >= group ~ 1,
    TRUE ~ 0)
  ) |>
  # create releative event-time indicator D_it_k
  mutate(d_it_k = case_when(
    group == 0 ~ Inf,
    TRUE ~ year - group)
  )


# Static model
result <- did2s(
  job_displacement_data,
  yname = "income",
  first_stage = ~ occ_score | id + year, # only time-variant covariates
  second_stage = ~ d_it,
  treatment = "d_it",
  cluster_var = "id"
)

fixest::esttable(result)


# Event Study
result <- did2s(
  job_displacement_data,
  yname = "income",
  first_stage = ~ occ_score | id + year, # only time-variant covariates
  second_stage = ~ i(d_it_k, ref = c(-3, Inf)),
  treatment = "d_it",
  cluster_var = "id"
)

# Dynamic TWFE
twfe <- feols(income ~ i(d_it_k, ref = c(-3, Inf)) + occ_score | id + year,
              data=job_displacement_data,
              cluster=c("id", "year"))

fixest::iplot(list(result, twfe), main = "Event study: Staggered treatment", 
              xlab = "Relative time to treatment", col = c("#005e73", "#00C1D4") , ref.line = -0.5)
# Legend
legend(x=5, y=30000, col = c("#005e73", "#00C1D4"), pch = c(20, 17), 
       legend = c("Two-stage estimate", "Dynamic TWFE"))

OLS estimation, Dep. Var.: income
Observations: 11,448
Standard-errors: Custom 
     Estimate Std. Error  t value  Pr(>|t|)    
d_it -5900.79    2151.88 -2.74215 0.0061132 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RMSE: 15,051.3   Adj. R2: 0.006894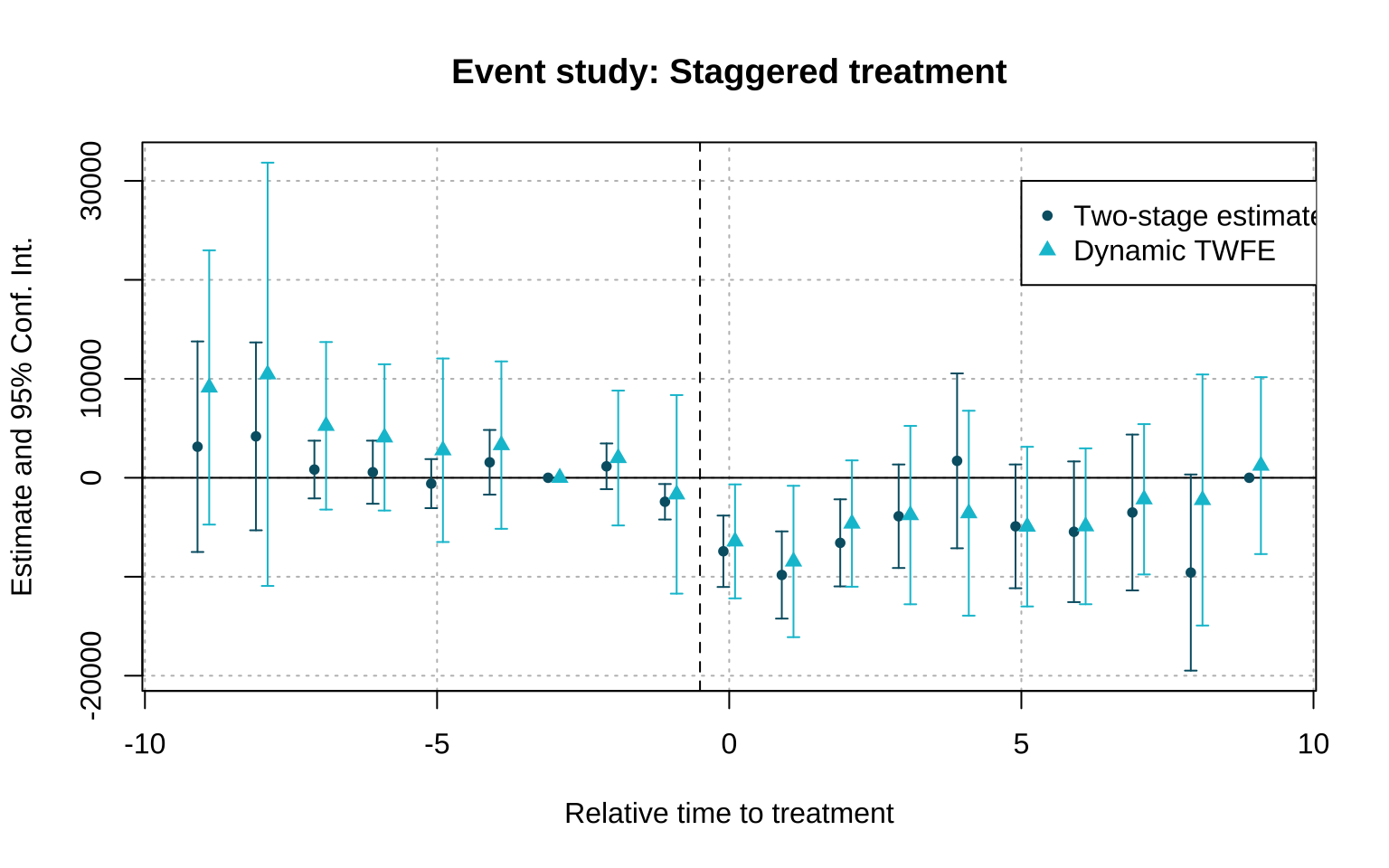

Testing for Parallel Trends

Testing for Pre-existing Trends

In most DiD applications we have several periods before anyone was treated.
We can test whether the groups were moving in parallel prior to the treatment.
- If so, then assumption that confounding factors are stable seems more plausible.
- If not, then it’s relatively implausible that would have magically started moving in parallel after treatment date.
Event study plot is a common way to visualize pre-trends, which van be generated based on:
- Dynamic TWFE (not robust with staggered timing).
- Comparision-based estimators.
- Imputation-based, two-stage estimators.

Issues with Pre-existing Trends (Roth, 2022)

Parallel pre-trends don’t necessarily imply parallel (counterfactual) post-treatment trends.
- If other policies change at the same time as the one of interest can produce parallel pre-trends but non-parallel post-trends.
Low power: even if pre-trends are non-zero, we may fail to detect it statistically
Distortions from pre-testing: if we only analyze cases without statistically significant pre-trends, this introduces a form of selection bias (pre-test bias which can make things worse).
If we fail the pre-test, what next? May still want to write a paper (especially if violation is “small”).

Issues with Pre-existing Trends (Roth, 2022)

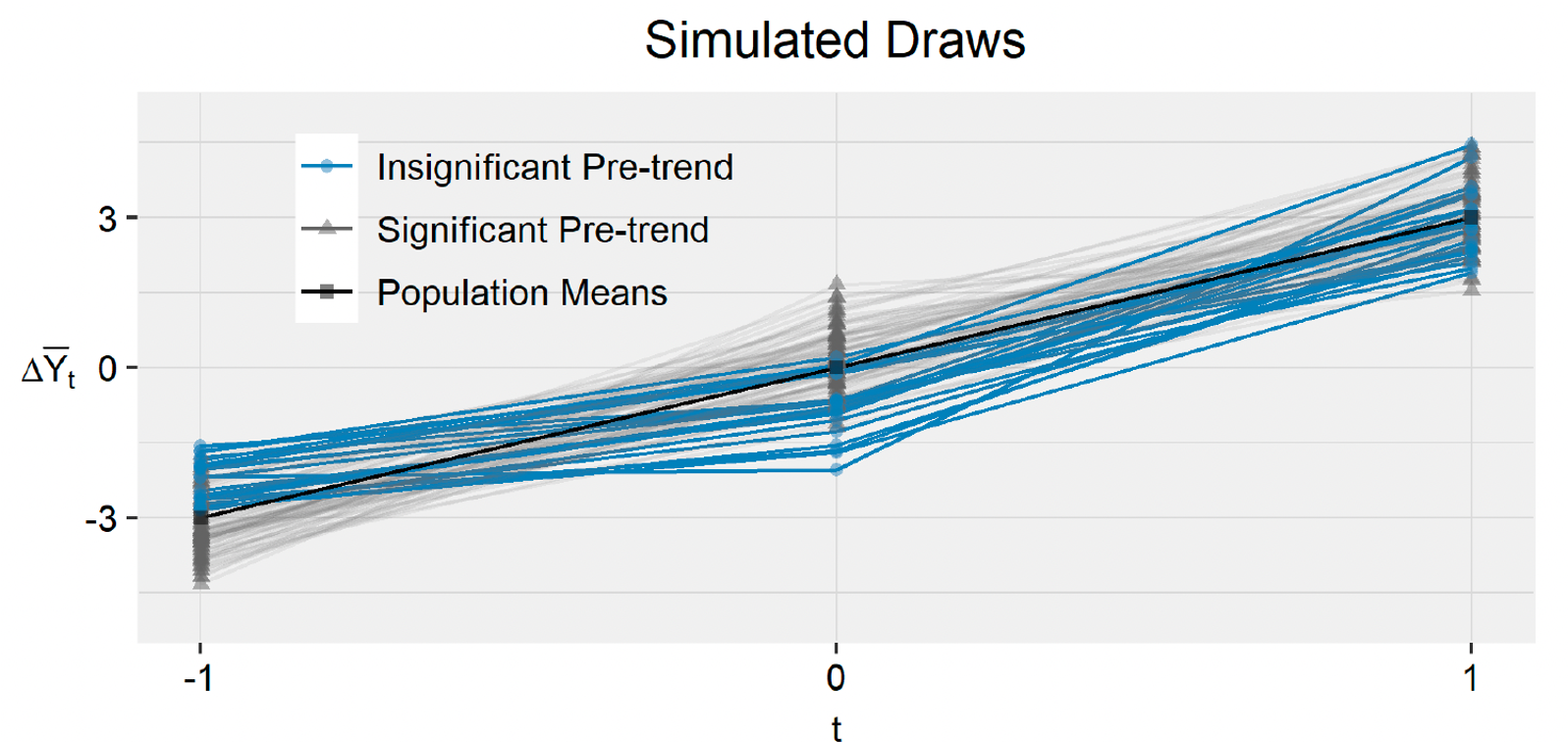
Power issues in pre-trend testing: We can’t reject zero pre-trend, but we also can’t reject pre-trends that under smooth extrapolations to the post-treatment period would produce substantial bias.

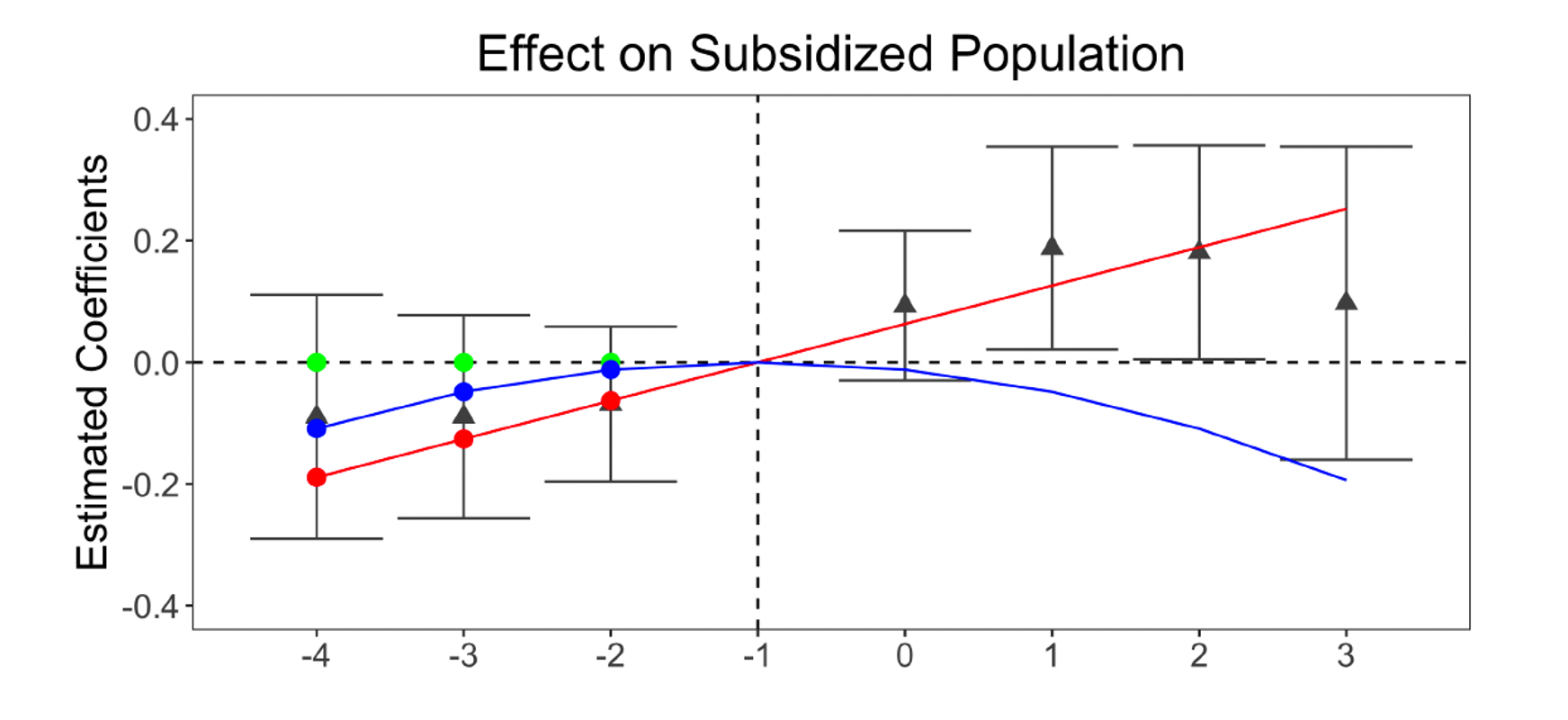
Distortions from pre-testing: If we happen to draw sample from the population where pre-trends are insignificant, the treatment effect we discover later on might be significantly biased (upwards in this example).

Solutions to Parallel Trends Testing

Roth (2022):
- Diagnostics of power and distortions from pre-testing.
  - Power: calculates the slope of a linear violation of parallel trends that a pre-trends test would detect a specified fraction of the time.
  - Distortions: calculates the bias that would result from only analyzing cases with statistically significant pre-trends.
- R package ‘pretrends’
Rambachan and Roth (2022):
- Formal sensitivity analysis that avoids pre-testing:
  - Put bounds to the unobservable post-treatment trend: how different could it be from the pre-treatment trend to invalidate the DiD estimate?
- R package ‘HonestDiD’

Thank you for your attention!
	startupengineer.io/authors/ihl christoph-ihl christophihl Ihluminate